Defining Convolution

Convolution is a mathematical operation that allows you to merge two entities to produce a third. The first entity could be a mathematical function, an audio signal, a 2D image, or any other relevant data. The second entity might be another function that performs a transformation or a probability distribution.

Mathematically, convolution is represented as F * G. It involves summing the product of F with the reverse of G. Quite straightforward, right?

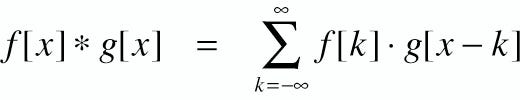
Typically, this is how professors present convolution, which can be quite intricate. Let me simplify it a bit. Please note that I am not a mathematics PhD, so I apologize in advance for any inaccuracies or oversights. I'm just a retiree revisiting college-level mathematics.

Visualizing Convolution with Dice

A simple way to conceptualize convolution is by summing the outcomes of two dice. For instance, if you roll two dice, what are the odds for each possible sum? Intuitively, we know there are 36 possible outcomes, with the sums of 2 and 12 each having a probability of 1/36, while the sum of 7 has the highest likelihood at 6/36.

To illustrate this, imagine sliding two sets of dice across one another. Starting with the 1s, we find that the probability of rolling a 2 is calculated by multiplying 1/6 by 1/6. Notice that the bottom set of dice is oriented backward; this is intentional to help align the probabilities as we move through the sums.

As we shift the bottom dice, we can calculate the probability of obtaining a sum of 3 by adding the combinations of rolling a 1 and 2 or a 2 and 1.

Continuing this process, we eventually arrive at the sum of 7, which can be rolled in six different combinations out of 36.

We can keep sliding until we reach sums of 8, 9, 10, and so on.

Eventually, we conclude with the sum of 12, which again has a probability of 1/36.

In a multiplication table, we observe that the likelihood of rolling any number on dice A and B consistently equals 1/6 * 1/6 = 1/36, which translates to approximately 0.027777777. The aggregated probabilities across rows, columns, and the table itself align logically.

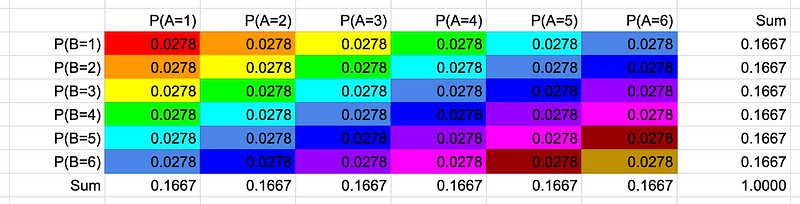
By summing the diagonals, which reflect the sliding motion of the two dice sets, we achieve the "convolution" result. It's noteworthy that the length of the convolution output equals (length of A) + (length of B) - 1. For two dice, this results in 6 + 6 - 1 = 11.

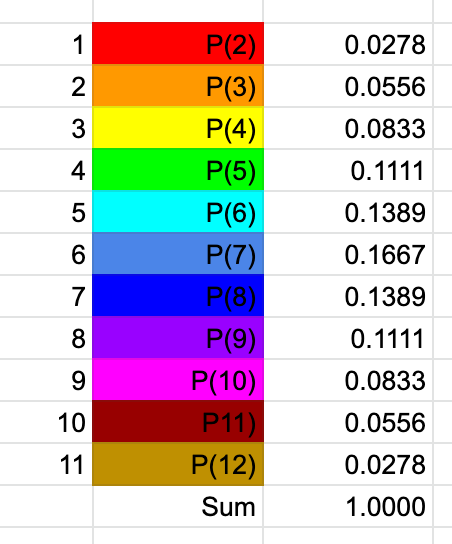
Exploring Uneven Dice

Now, let's introduce some complexity. What if the dice were uneven, with varying probabilities for each number? How would we determine the odds of their sums?

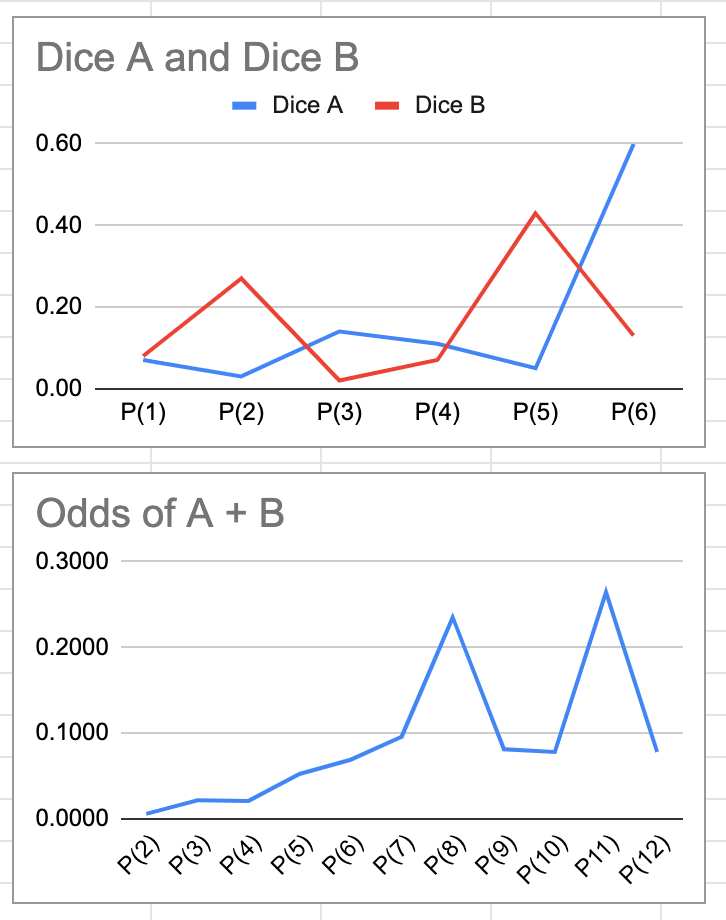
Assume the following distributions for our dice: Dice A has a high chance of landing on 6, while Dice B is more likely to roll a 2 or a 5. Logically, we would anticipate that the sums of 8 and 11 would yield the highest probabilities.

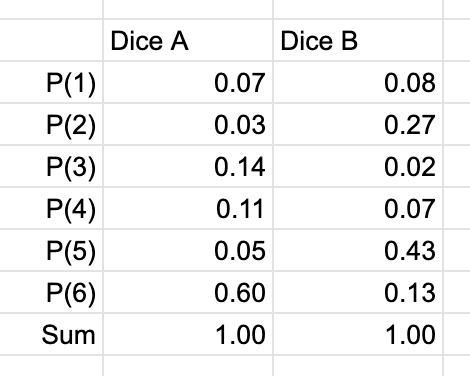
The multiplication table for these outcomes appears as follows:

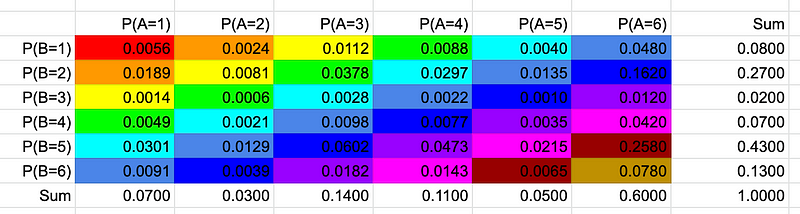
By summing the diagonals, we find that indeed, 8 and 11 have the highest probabilities, confirming our initial hypothesis.

Graphically, this is represented in a line chart. Convolution enables us to merge two signals into a new signal as their product, even when considering uneven probabilities. Quite fascinating, isn't it?

Applying Convolution in Programming

This convolution technique can also be valuable for calculating moving or weighted averages, particularly in programming or statistics interviews.

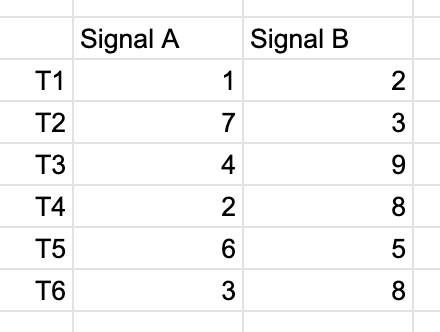
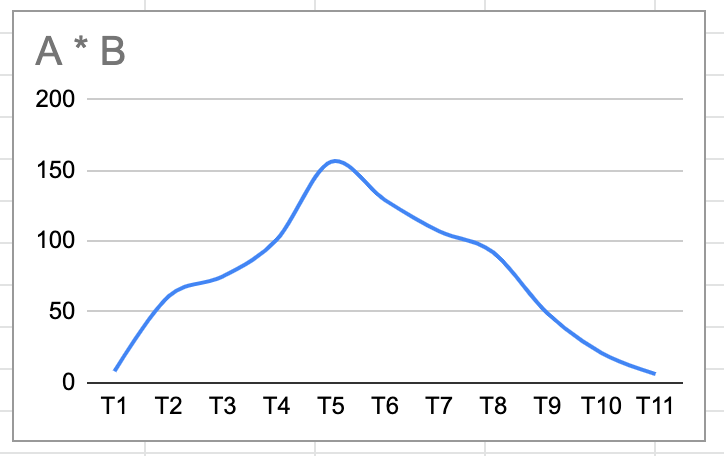
Next, let's shift our focus to regular whole numbers instead of decimals. Below are two signals, A and B, measured from time T1 to T6.

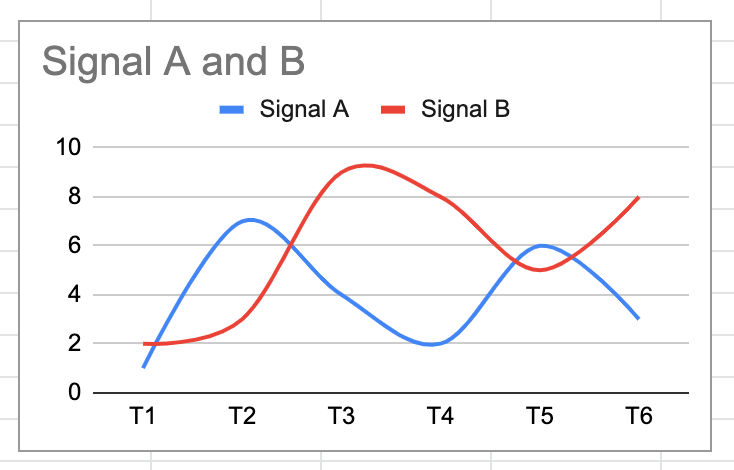
Visually, they can be depicted with a smooth line chart.

To compute the convolution, we reverse B and multiply it into A, summing across time T (in seconds). Remember, the result will contain 6 + 6 - 1 = 11 points! This indicates that it would take 11 seconds for both 6-second signals to completely overlap. Makes sense, right?

Here's the resulting convolution, where you can see the shape of line A as line B interacts with it.

Understanding Curves

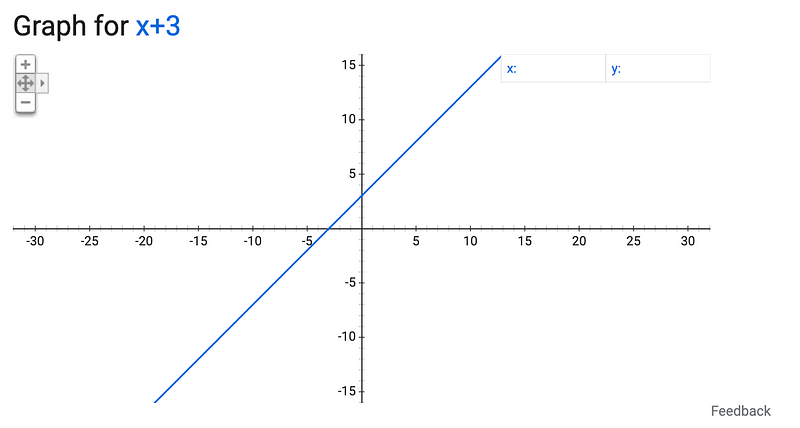
Let’s revisit Algebra for a moment. What kind of line do you obtain from a linear equation, such as y = x + 3? It forms a straight line.

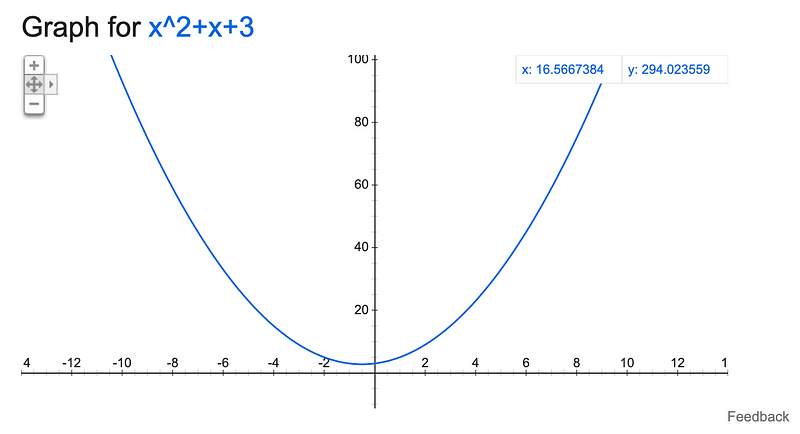
What about a quadratic equation? You get a U-shaped curve.

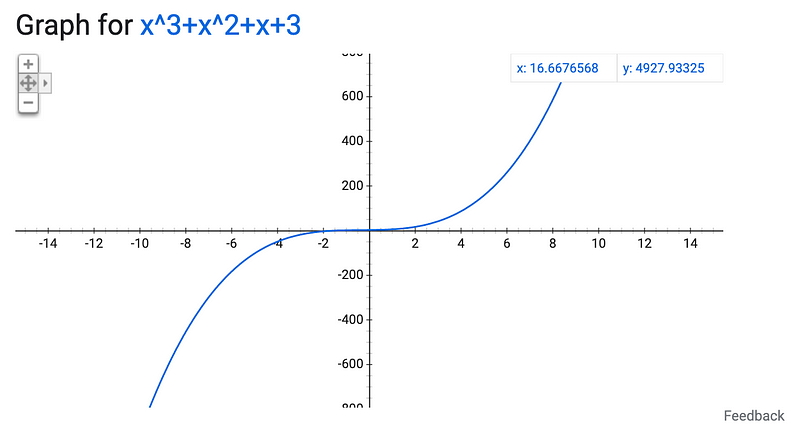
And a cubic equation? That results in a sideways S shape.

Are you noticing the trend? Any curve or signal can be depicted by a polynomial equation of degree N, which corresponds to N-1 bends. For instance, a fifth-degree polynomial could appear as follows (with four bends):

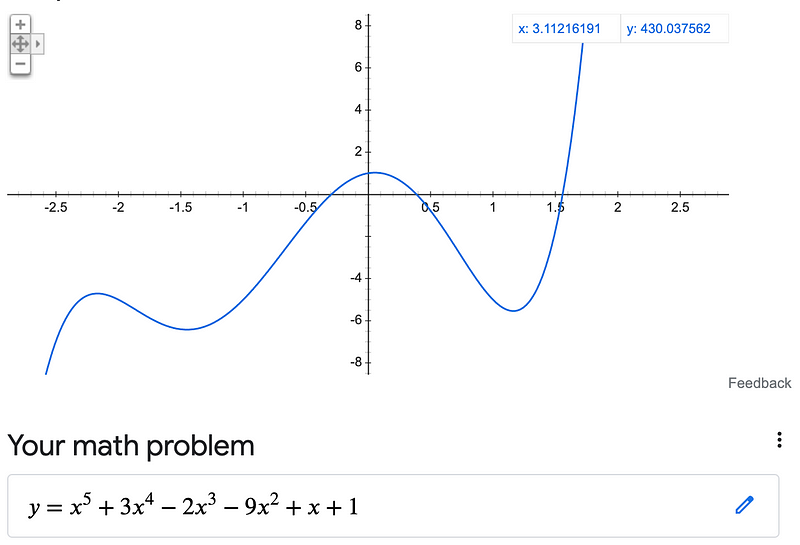
Representing Polynomials in Convolution

If a signal resembles a polynomial, then convolution is essentially the multiplication of two polynomials. Let's consider two polynomials that we wish to multiply:

(3x² + 6x + 2x³ + 4x² + 7x + 1) * (8x² + 5x + 8x³ + 9x² + 3x + 2)

Both polynomials are of fifth degree with a length of 6, meaning the final result will be a tenth-degree polynomial with a length of 11, akin to our previous examples with dice and signals.

To visualize this, we will write the polynomials in ascending order of power, e.g., a + bx + cx². Next, we reverse the second polynomial, slide, and multiply it over the first, followed by summing the terms.

This approach is easier to comprehend through examples.

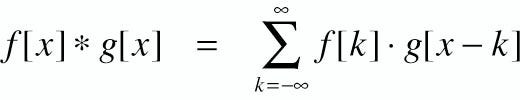
Notice how we reversed the second polynomial, allowing the x-powers to align as we slide, making the summation far more manageable.

Does the convolution equation begin to clarify? This is why f[k] is multiplied by g[x-k]. The convolution equation multiplies f with the reversed g and then sums the results. Visualizing polynomials aids in understanding the equation!

Confirming with Python

If we apply this to time series, how would you multiply two time series f and g? You would need to reverse time series g so that T0 of f is multiplied with T0 of g as they overlap. This concept might seem strange, but it's the most effective way I've grasped it.

Completing the polynomial multiplication, we get:

1 + 7x + 4x² + 2x³ + 6x² + 3x

8x² + 5x + 8x³ + 9x² + 3x + 2

24x² + 63x + 70x + 117x + 155x + 117x + 115x + 87x³ + 38x² + 17x + 2

Just to validate this in Python, the numpy.convolve function yields the exact same coefficients (listed from lowest power to highest).

This method is reciprocal as well.

Returning to Multiplication

Now that we've explored convolution through dice, signals, and polynomials, I hope you see why g must be reversed for effective multiplication.

But how does this relate to multiplying large numbers? Consider the polynomial example from earlier. If we let x equal 10, what have we just solved?

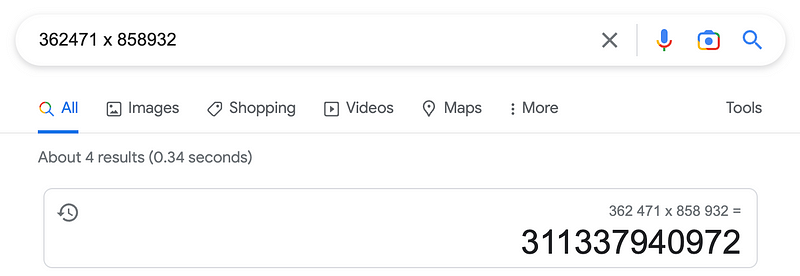
We effectively computed 362471 x 858932 using convolution. This method operates similarly to traditional long multiplication.

Want evidence? Here's the multiplication table employing the coefficients of the two polynomials.

When summed up, we obtain…

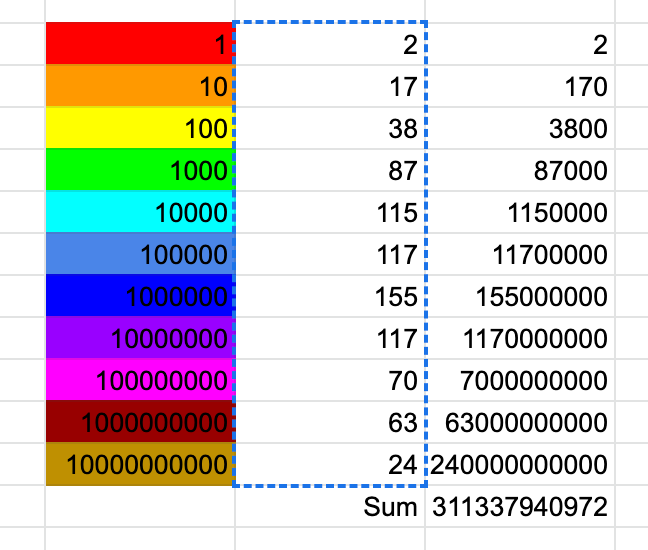
And, as expected, the math checks out.

The Final Insights

Utilizing standard multiplication and addition in convolution results in O(N²), which is no faster than conventional long multiplication or even the Karatsuba Method.

However, the Fast Fourier Transform (FFT) provides an optimized algorithm for convolution, achieving O(N log N) due to its recursive nature and symmetric properties around the unit circle. Don't worry if you find this last point confusing; it took me a while to understand it too! Once I gain clarity, I plan to write another article to explain it further.

The essential takeaway is that convolution is a powerful operation for "multiplying" two signals, which can be represented by polynomial equations with a base of 10. When viewed through this lens, large numbers can be multiplied via convolution, and using FFT makes this process the fastest available.

(Note: The Schönhage–Strassen algorithm employs FFT in a manner that exceeds my current understanding.)

By integrating these techniques, mathematicians and computer scientists have unlocked the potential of large numbers for applications such as modern encryption methods.

What a remarkable, awe-inspiring, and beautiful discovery!