Chapter 1: The Beauty of Physical Laws

While it's true that not every law of physics is visually appealing, many enthusiasts of physics and mathematics share a belief in the intrinsic beauty of these fields. This perspective is often referred to as the "beauty argument." Notably, physicist Richard Feynman emphasized this sentiment by stating,

“It doesn’t matter how beautiful your guess is, how intelligent the person making the guess is, or what their name is. If it contradicts experimental results, it’s incorrect.”

The "beauty argument" suggests that Nature is best expressed through equations that possess an aesthetic quality. This belief can be traced back to an insightful interview involving Paul Dirac, where he remarked,

“The concept of spin emerged from exploring equations rather than imposing physical notions. Much of my work involves playing with equations to uncover beautiful mathematical relationships, some of which might lack physical significance.”

In a 1982 paper titled "Pretty Mathematics," Dirac suggested that it is a fundamental characteristic of nature that basic physical laws can be articulated through a mathematically elegant framework. He noted that one might say God is a mathematician of the highest order, using advanced mathematics to construct the universe. He posited that pursuing beauty in equations often leads to substantial insights and progress.

Mathematics serves as a versatile language, allowing skilled mathematicians to create new terminologies and grammatical structures that transform previously unattractive concepts into something beautiful. A prime example is Maxwell’s equations, which were initially presented in a less appealing manner. The reformulation by Oliver Heaviside introduced a more aesthetically pleasing syntax that we recognize today.

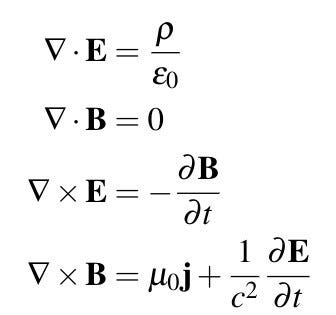
Section 1.1: The Role of Aesthetic in Mathematics

Mathematical beauty is not merely for show; it clarifies the meanings within equations and facilitates the derivation of new results. A more succinct equation can often illuminate concepts better than a more verbose one. One can liken an elegant mathematical expression to poetry, whereas a more detailed version resembles prose.

To illustrate this, consider Charles Dickens' vivid description from "The Pickwick Papers":

“That punctual servant of all work, the sun, had just risen, and begun to strike a light on the morning of the thirteenth of May, one thousand eight hundred and twenty-seven, when Mr. Samuel Pickwick burst like another sun from his slumbers, threw open his chamber window, and looked out upon the world beneath.”

Here, the reader is transported to the scene, vividly experiencing the sunrise alongside Mr. Pickwick. In contrast, a haiku by Yosa Buson encapsulates an entire scene in just a few words:

“Such a moon! The thief pauses to sing.”

This brief expression evokes a rich imagery, allowing the reader to perceive the moon, the night, and even the atmosphere surrounding the thief.

Chapter 2: The Intersection of Art and Science

In this TEDx talk, Naeem Fazal explores the profound connection between beauty and science, emphasizing the aesthetic dimensions of physical laws.

Jordan Peterson discusses the significance of beauty in understanding the universe, merging philosophical ideas with scientific principles.