Understanding Equations through Functions

The most straightforward method to investigate an equation is to formulate a function that performs the calculations. This function will accept various parameters, each assigned a default value.

By setting default values for the parameters, we can selectively modify the parameters of interest without needing to re-enter them each time. For instance, to alter the <code>rt</code> parameter, we would invoke the function as follows: <code>archie_sw(rt=100)</code>.

def archie_sw(a=1, phi=0.15, m=2, rw=0.2, rt=200, n=2):

Sw = ((a / phi**m) * (rw / rt))**(1/n)

return Sw

Initially, if we call the function without providing any parameters, the default values will be employed.

archie_sw()

This will yield an Sw value of:

0.21081851067789195

By adjusting parameters like tortuosity (<code>a</code>) and porosity (<code>phi</code>):

archie_sw(a=1.2, phi=0.25)

We obtain a new Sw value of:

0.13856406460551018

While this method simplifies exploring the Archie equation's parameters, it can become laborious and time-consuming to continually modify values and re-execute the cells.

Enhancing Interactivity with ipywidgets

To alleviate the need to rerun the function every time we wish to modify a parameter, we can introduce interactive widgets within our notebook.

This is achieved by importing widgets from <b>ipywidgets</b> and establishing several sub-widgets linked to each parameter.

First, we need to import the necessary modules: <code>widgets</code> from <code>ipywidgets</code> and <code>display</code> from <code>IPython.display</code> to visualize our widgets in the notebook.

Next, we define our Archie Water Saturation equation along with its parameters. This function is subsequently invoked within the <code>update_widget</code> function.

Lastly, we can configure the type, default values, and acceptable ranges for the widgets we wish to display.

import ipywidgets as widgets

from IPython.display import display

# Archie's Equation function

def archie_sw(a, PHI, m, Rw, Rt, n):

Sw = ((a / PHI**m) * (Rw / Rt))**(1/n)

return Sw

# Interactive widget

def update_widget(a=1, PHI=0.2, m=2, Rw=0.1, Rt=2, n=2):

Sw = archie_sw(a, PHI, m, Rw, Rt, n)

print(f"Water Saturation (Sw): {Sw:.2f}")

widgets.interact(update_widget,

a=widgets.FloatSlider(value=1, min=0.1, max=5, step=0.1, description='a:'),

PHI=widgets.FloatSlider(value=0.2, min=0.01, max=0.4, step=0.01, description='PHI:'),

m=widgets.FloatSlider(value=2, min=1, max=4, step=0.1, description='m:'),

Rw=widgets.FloatSlider(value=0.1, min=0.01, max=1, step=0.01, description='Rw:'),

Rt=widgets.FloatSlider(value=2, min=1, max=100, step=1, description='Rt:'),

n=widgets.FloatSlider(value=2, min=1, max=4, step=0.1, description='n:'))

Upon executing the above cell in our notebook, the interactive sliders will be presented.

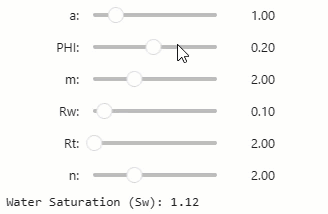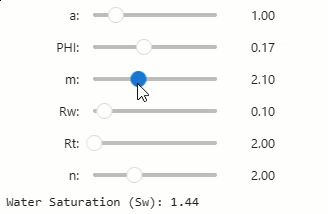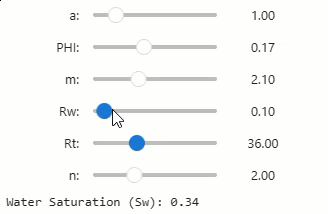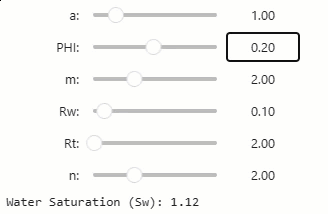
Adjusting any of the sliders will automatically update the resulting Sw value.

Employing ipywidgets in Jupyter (Dataframe + Log Plot)

In petrophysical interpretations, we often deal with continuous data instead of a single data point. The previous approach is effective for analyzing each parameter's influence on a singular Sw value.

We can broaden our previous example by incorporating real-world data and constructing a basic log plot that dynamically updates when parameters are modified.

In this instance, utilizing the publicly accessible Volve dataset, we have a porosity (<code>phi</code>) curve and a resistivity (<code>rt</code>) curve, both vital inputs for the Archie water saturation equation.

The other parameters can be adjusted to illustrate their effects across an entire reservoir section.

In the top subplot (track), we display the water saturation calculated with the default parameters to establish a baseline. This is juxtaposed with results derived from the interactive parameters.

To create the plot illustrated above, you can use the following code:

import pandas as pd

import matplotlib.pyplot as plt

import ipywidgets as widgets

from IPython.display import display

df = pd.read_csv('../data/Volve/15_9-19.csv', usecols=['DEPTH','PHIT', 'GR', 'RT'], na_values=-999)

# Extract a small depth interval

df = df.query('3800 <= DEPTH <= 4100')

def archie_sw(a=1, phi=0.15, m=2, rw=0.2, rt=200, n=2):

Sw = ((a / phi**m) * (rw / rt))**(1/n)

return Sw

df['SW_ARCH_BASE'] = df.apply(lambda row: archie_sw(phi=row['PHIT'], rt=row['RT']), axis=1)

@widgets.interact(a=(0.5, 1.5, 0.05), m=(1.5, 2.5, 0.05), rw=(0.1, 10, 0.1), n=(1.5, 2.5, 0.05))

def update_plot(a=1, m=2, rw=1, n=2):

depth = df['DEPTH']

df['SW_ARCH_NEW'] = df.apply(lambda row: archie_sw(phi=row['PHIT'], rt=row['RT'],

a=a, m=m, rw=rw, n=n), axis=1)

fig, ax = plt.subplots(nrows=4, ncols=1, sharex=True, figsize=(20, 10))

ax[0].plot(depth, df['SW_ARCH_BASE'], c='k')

ax[0].plot(depth, df['SW_ARCH_NEW'], c='red')

ax[0].fill_between(depth, 1, df['SW_ARCH_NEW'], color='green')

ax[0].fill_between(depth, 0, df['SW_ARCH_NEW'], color='skyblue')

ax[1].plot(depth, df['RT'], c='k')

ax[2].plot(depth, df['PHIT'])

ax[3].plot(depth, df['GR'], c='green')

ax[0].set_ylim(0, 1.0)

ax[1].semilogy()

ax[2].set_ylim(0, 0.5)

ax[3].set_ylim(0, 150)

ax[0].set_ylabel('SW')

ax[1].set_ylabel('RT')

ax[2].set_ylabel('PHIT')

ax[3].set_ylabel('Gamma')

plt.show()

Summary

The more interactive your learning experience, the greater the likelihood of retaining the information acquired.

In this article, I have demonstrated three straightforward yet effective methods to utilize Python for comprehending a fundamental equation in petrophysics. By allowing interactivity with the parameters in the final example, we can examine their impacts on actual data.

Dataset Utilized

The data presented in this tutorial is a subset from the Volve Dataset released by Equinor in 2018. Full details, including the license, can be accessed via the link below:

Volve field dataset download — Equinor

The Volve data is licensed under the CC BY 4.0 license. Comprehensive details of the license agreement can be found here:

https://cdn.sanity.io/files/h61q9gi9/global/de6532f6134b9a953f6c41bac47a0c055a3712d3.pdf?equinor-hrs-terms-and-conditions-for-licence-to-data-volve.pdf

Thank you for reading. Before you leave, don't forget to subscribe to my content to receive my articles directly in your inbox. You can do that here! If you enjoyed this article and wish to show your appreciation, please consider giving it a few claps.