Understanding Euler's Theorem: A Comprehensive Guide
Written on
Chapter 1: Introduction to Euler’s Theorem
Euler's Theorem stands as a foundational concept in number theory, often introduced early in mathematical studies. The theorem can be succinctly stated as follows:
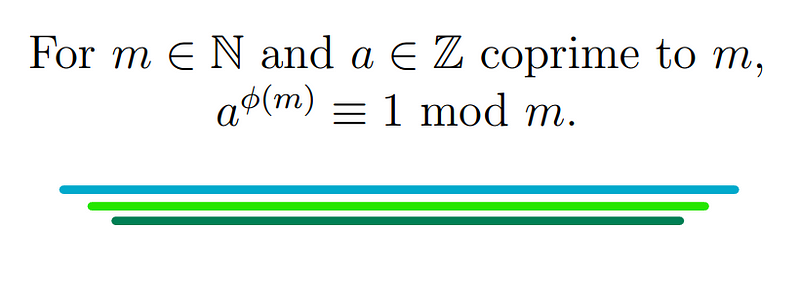
The function ?(m) is defined to count the integers less than m that are coprime to m, meaning they share no common factors with m. For instance, ?(10) equals 4. The theorem asserts that for any positive integer m and any integer a, raising a to the power of ?(m) yields 1 modulo m (i.e., one more than a multiple of m).
In this discussion, I will present two distinct proofs of this theorem, beginning with the more complex one. It's worth noting that the simpler proof relies on abstract algebra concepts that first-year students may not yet grasp. Let's delve into the more intricate proof first:
Section 1.1: Proof 1 - The Complex Approach
We analyze numbers of the form ka, where (1 leq k < m) and k is coprime to m. Since these k values are all the positive integers less than m that are coprime to it, multiplying them by a, which is also coprime to m, results in all the kas remaining unique modulo m and coprime to m.
Next, we take the product of these values, as follows:
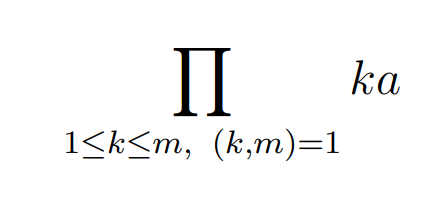
Here, (k, m) represents the greatest common divisor of k and m, which equals one when k and m are coprime. As we are calculating the product over specific k values, we can extract the constants from the product. To achieve this, we need to determine how many k values we are multiplying together.
Recalling that ?(m) counts the number of positive integers less than m that are coprime to m, we find that the product multiplies ?(m) terms. This leads us to the conclusion that:
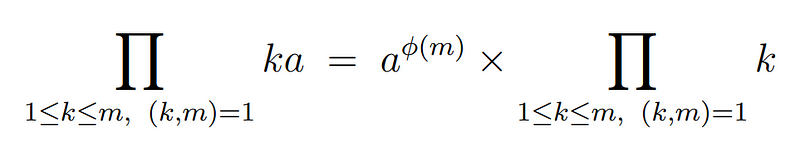
Earlier, I stated that all kas are unique modulo m and coprime to m, just as the ks are. This gives us the following equality modulo m:
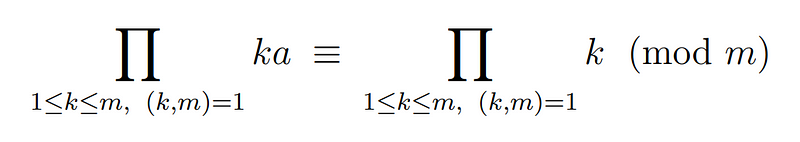
We can now merge the two equalities:
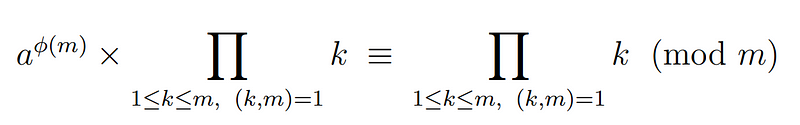
Ultimately, we can divide both sides by the product of ks, which is permissible since this product remains coprime to m.
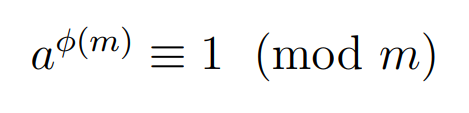
This achieves the desired outcome, concluding the proof. It may seem like a convoluted mess of modulo arithmetic and products, yet it is gratifying in its resolution.
Section 1.2: Proof 2 - The Simplified Approach
Now, let's explore the second, more straightforward proof. This proof does require a basic understanding of group theory, particularly Lagrange’s theorem.
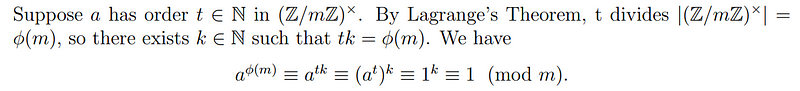
This proof is considerably shorter but slightly more technical. The question arises: which is more challenging? The long, intricate product and modulo arithmetic, or mastering Lagrange’s Theorem?
Chapter 2: Additional Resources
To enhance your understanding of Euler's Theorem and number theory, consider these insightful videos.
The first video, titled "9 Tips to Help You PROVE MATH THEOREMS," offers practical advice for proving mathematical concepts and theorems effectively.
The second video, "New Orleans Teens Make Mathematical Discovery Unproven for 2,000 Years," showcases a remarkable mathematical breakthrough by young minds, emphasizing the ongoing relevance of number theory.