Modeling a Realistic Bouncing Ball with Springs
Written on
Chapter 1: Understanding the Basics of Bouncing Balls
When you drop a ball, it bounces back up, but it never quite reaches the original height. Even the most resilient “super bounce” balls can't achieve this. The reason lies in the conversion of gravitational potential energy into kinetic energy as the ball descends. Upon hitting the ground, some of that energy transforms into thermal energy, leading to a loss in total energy available for the upward bounce. By measuring the initial and peak heights, you can determine the coefficient of restitution, which quantifies the bounce efficiency. Here’s my data related to this phenomenon.
How can we effectively create a model that mimics the behavior of a real bouncing ball? Instead of simply adjusting kinetic energy after each bounce, let's explore a more fundamental approach.
Section 1.1: The Ideal Bouncing Ball Model
To begin, let’s construct a model of an ideal bouncing ball that falls, strikes the ground, and rebounds to its original height. This model will utilize a spring as the ground. The impact will compress the spring, allowing it to store elastic potential energy, which then converts back to kinetic energy, enabling the ball to bounce back to the original height.
This process can be represented through numerical calculations. We'll divide the problem into small time intervals, assuming a constant force during each interval to calculate momentum changes, and then maintain that momentum to determine position changes. The cycle repeats for subsequent intervals.
For those interested in the numerical approach, I use Glowscript, which is an enhanced version of Python. To dive deeper into this method, check out this video tutorial.
Section 1.2: Constructing a Simple Bouncing Ball Model
Next, let’s develop a straightforward bouncing ball model. In this instance, our ball will be a solid object impacting a perfect spring embedded in the floor. The floor is designed to be partially transparent to visualize the spring beneath.
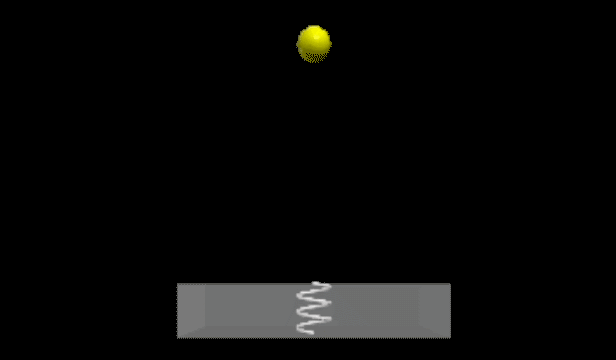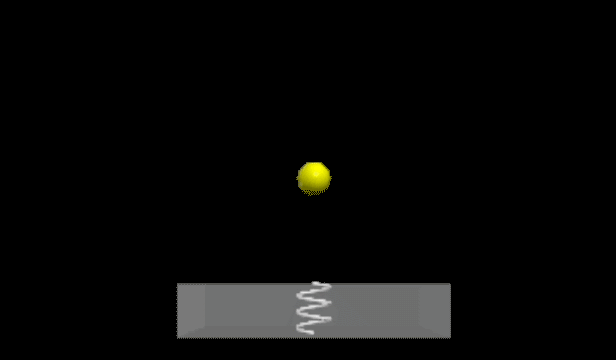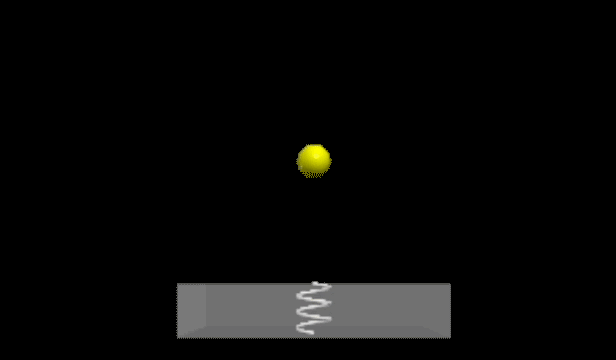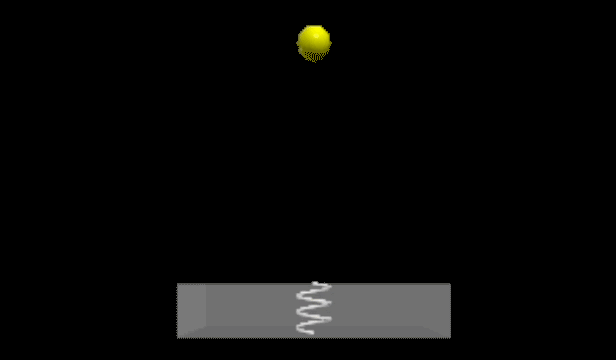
Chapter 2: Advancing the Bouncing Ball Model
To illustrate a more complex bouncing ball scenario, we'll employ a concept suggested by a fellow physics professor. Instead of a single ball, we will utilize two balls, each with half the mass of the original. These two balls will be interconnected by a spring, as depicted below.
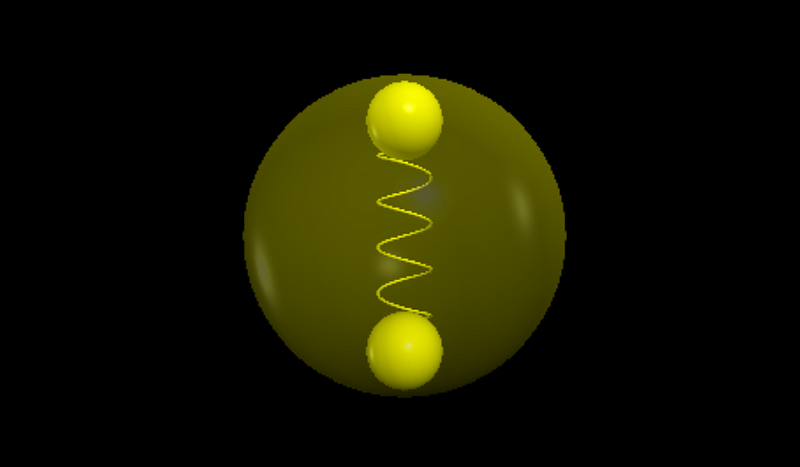
Upon dropping this “ball,” the two interior masses will initially be separated, allowing the internal spring to remain relaxed. However, when the lower mass makes contact with the floor-spring, the internal spring compresses. As the ball rebounds, different dynamics come into play.
Let’s take a closer look at the behavior of this model.
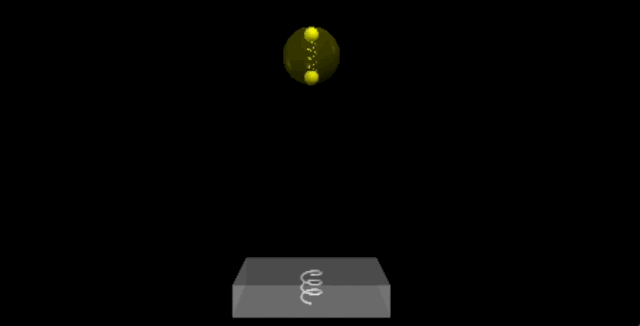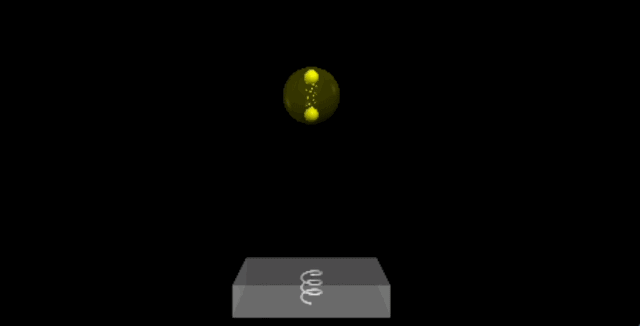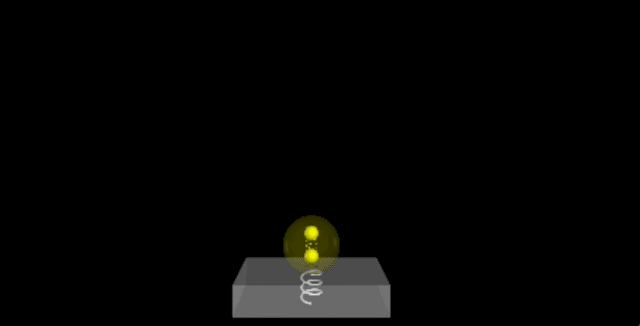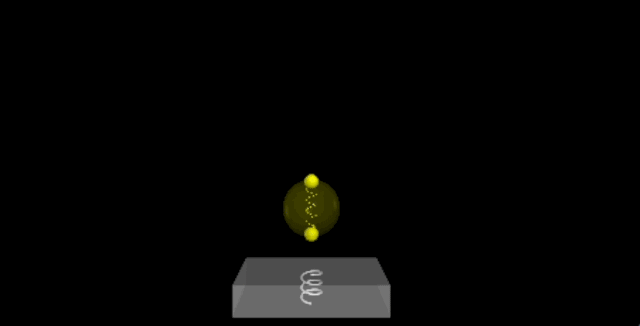
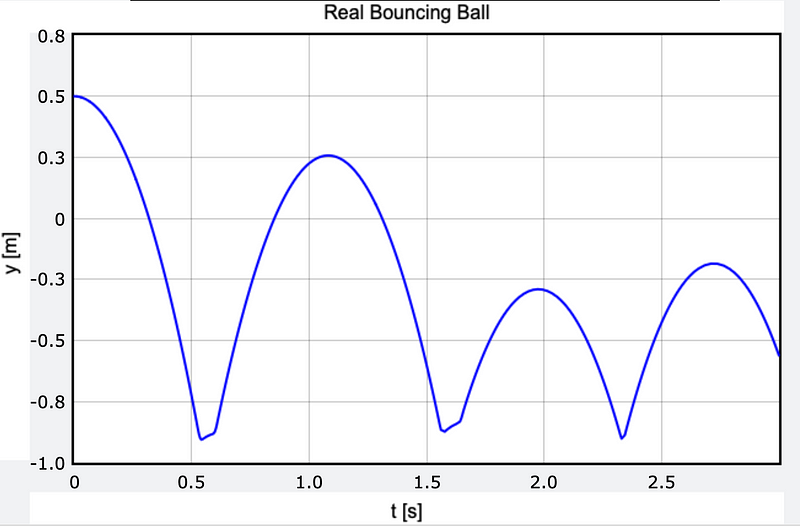
After three bounces, the model displays intriguing behavior. Although some oscillation occurs, the rebound height decreases with each impact, resembling the behavior of real-world balls. The following plot illustrates the vertical position of the ball's center, calculated using the center of mass of the two internal balls.
What's fascinating here is the energy dynamics. Although the bounce height decreases, this doesn’t imply energy loss. The system includes the Earth, the floor spring, and both balls, contributing various forms of energy: kinetic energy, gravitational potential energy, and elastic potential energy in both springs.
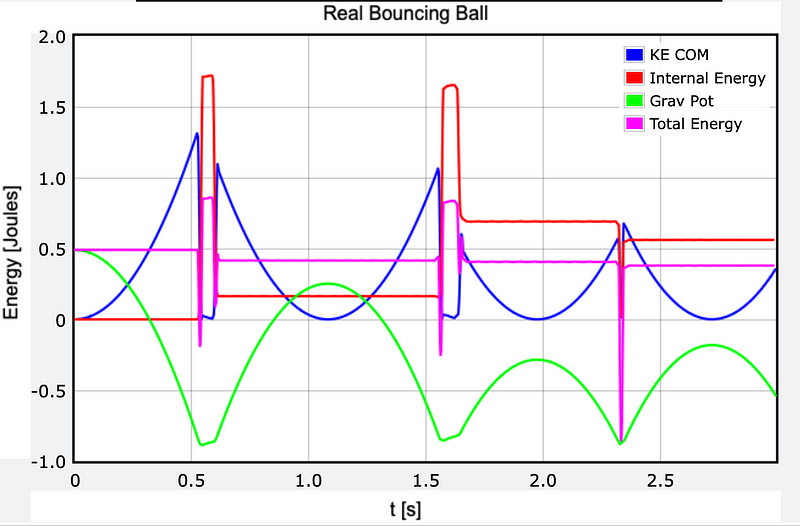
The graph illustrates several key features. The magenta line represents the total energy, which remains fairly stable, while the red curve denotes internal energy, rising upon impact. This increase accounts for the reduction in center of mass kinetic energy, preventing the ball from achieving the same height on subsequent bounces.
To summarize, this model demonstrates a bouncing ball that does not reach the same height after each impact. Here are two potential homework projects for further exploration.
HW 1: Investigating Rotational Dynamics
Imagine a similar model but tilted so that the lower ball isn't directly under the upper one. When this tilted ball hits the floor, it should rotate, introducing rotational kinetic energy. How would this altered model behave compared to the original? Consider modeling it in Python.
HW 2: Exploring Multiple Balls
In the previous model, we utilized two balls. What happens if we expand this to eight balls surrounding a central one?
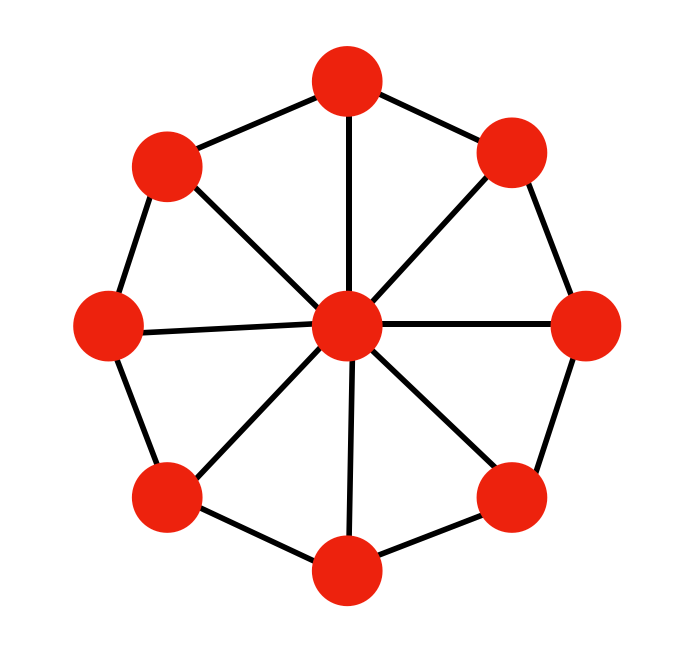
Constructing and analyzing this configuration could yield fascinating insights into bouncing dynamics.