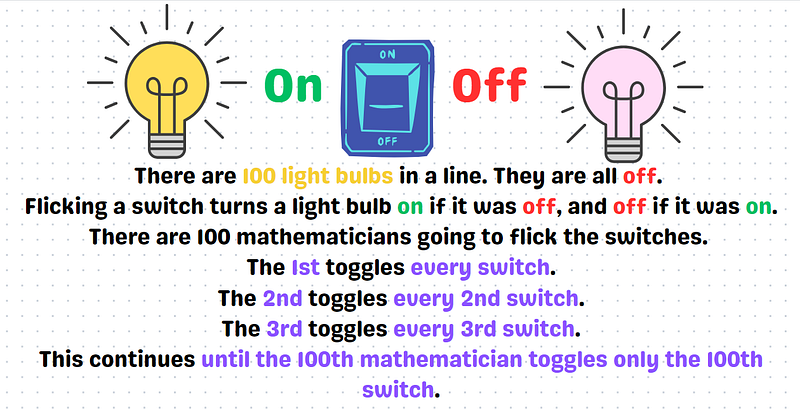
Exploring the Mystery of Light Bulbs and Mathematicians
Written on
Chapter 1: The Puzzle Begins
Recently, I completed all three seasons of the Netflix series Travelers. The show revolves around preserving humanity's future by making changes in the past. The director accomplishes this by transferring the consciousness of specially trained operatives from the future into the bodies of people living in the present. These operatives are referred to as "Travelers."
Perhaps I can elaborate on the series later! For now, let's dive into a puzzle: how many light bulbs remain illuminated? I suggest you pause here, grab a pen and paper, and give it a try. Once you're ready, continue reading for the solution!
Solution
To tackle this puzzle, think about the switch being toggled whenever a mathematician's number is a factor of the locker number.
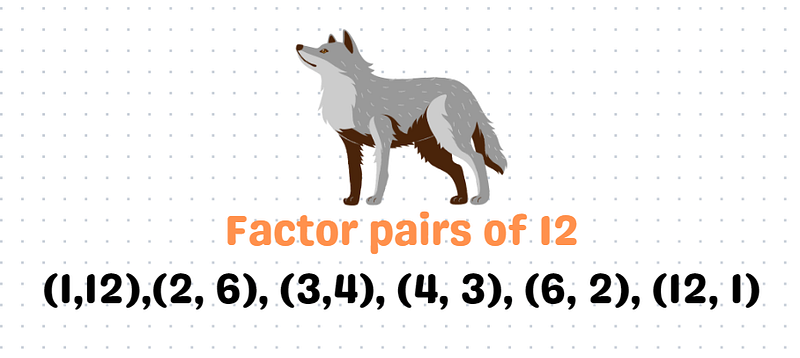
Extend this reasoning by selecting random counts of mathematicians, for example, 36 and 57. Let's particularly examine the 12th bulb.

In this case, the 1st toggle turns on the 12th bulb. The 2nd toggle turns it off. The 3rd toggle turns it back on, while the 4th toggle switches it off again. The 6th toggle will flip it one more time, and finally, the 12th toggle will turn it off. All other toggles will leave it unchanged, resulting in the final state being off.
It’s important to note that the nth toggle refers to the nth mathematician's action of flipping the switches.
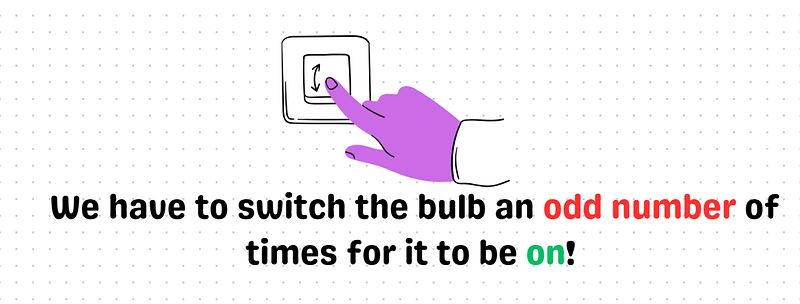
If you’ve run through a few scenarios in your mind, you may have noticed a connection to square numbers. Upon further reflection, you might realize that only square numbers possess an odd number of factor pairs.
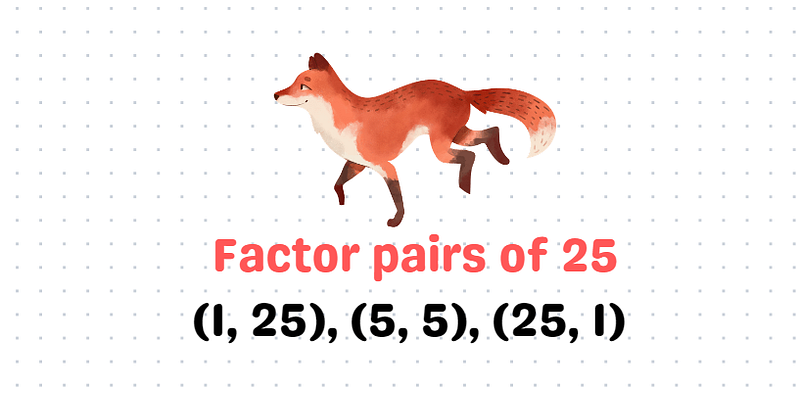
On-off toggling: Three toggles result in the bulb being on, which holds true for any odd number of toggles. Let’s consider 25 as an example; since 25 = 5², it qualifies as a square number.
The factor pairs of (1, 25) can be matched with (25, 1), while (5, 5) stands alone. All square numbers contain a factor pair with a repeated number, whereas non-square numbers do not, as they would otherwise be classified as square numbers.
Thus, it holds true that only square numbers have an odd number of factor pairs.
And that gives us our answer.

Isn’t it fascinating?
What were your thoughts while solving this? Feel free to share your insights below; I’d love to hear from you!
Math Puzzles
The best math puzzles on Medium
Algebra, Geometry, Calculus, Number Theory and more
Share this with your friends and...
Bella’s Weekly Math Games
A Weekly 48-Hour Math Competition
Stay updated with my latest articles by signing up for notifications. Thank you for your support!

Thank you for reading! If you found this piece informative, please give it a clap.

If you appreciate my work and feel inclined to support me, consider buying me a coffee. Your generosity greatly aids my writing and academic pursuits.
Happy Solving, Bella
If you'd like to connect professionally or just say hi, don't hesitate to reach out! I’m always open for a chat.
Chapter 2: Insights from Videos
In this video titled "Cambridge Ideas - How Many Lightbulbs?" we delve into the intriguing question of how many light bulbs remain on after a series of switches are flipped by mathematicians.
The second video, "Incandescent light bulbs now banned from being manufactured and sold in U.S." provides context on the evolution of light bulbs and the implications of this decision.