Unlocking the Secrets of the Universe: The Power of Polynomial Metrics
Written on
Chapter 1: The Mathematical Odyssey
Imagine entering a realm where every curve, surface, and shape adheres to a concealed, harmonious principle — a principle that is both fundamental and intricate, shaping the very essence of reality. This is the domain of locally symmetric polynomial metrics, where the abstract world of mathematics intersects with the tangible universe. As we embark on this mathematical odyssey, we will uncover the core concepts of Riemannian and Finslerian surfaces, exploring their secrets and profound effects on our comprehension of geometry and physics.
Section 1.1: Riemannian and Finslerian Surfaces
At the heart of our investigation lie the Riemannian and Finslerian surfaces, two foundational elements that underpin the vast expanse of geometric analysis. Riemannian surfaces, characterized by their gentle curvature and seamless transitions, provide insight into the elegant continuity of space. In contrast, Finslerian surfaces challenge our traditional notions with their asymmetric distances, pushing the limits of our understanding of ‘distance’ itself. Together, they create a duality of harmony and complexity, showcasing the beauty and challenges inherent in contemporary geometry.
Subsection 1.1.1: The Essence of Locally Symmetric Metrics

Symmetry, a concept as timeless as existence itself, finds fresh expression within locally symmetric metrics. These metrics unveil a reality where every point, curve, and surface embodies a universal order — a symmetry that transcends the local limitations of space. This intrinsic symmetry not only simplifies the intricate equations governing these surfaces but also opens new avenues for addressing long-standing challenges in mathematics and theoretical physics.
Section 1.2: The Visual Symphony of Symmetry
To further highlight the marvels of locally symmetric polynomial metrics, let’s delve into a captivating visualization:
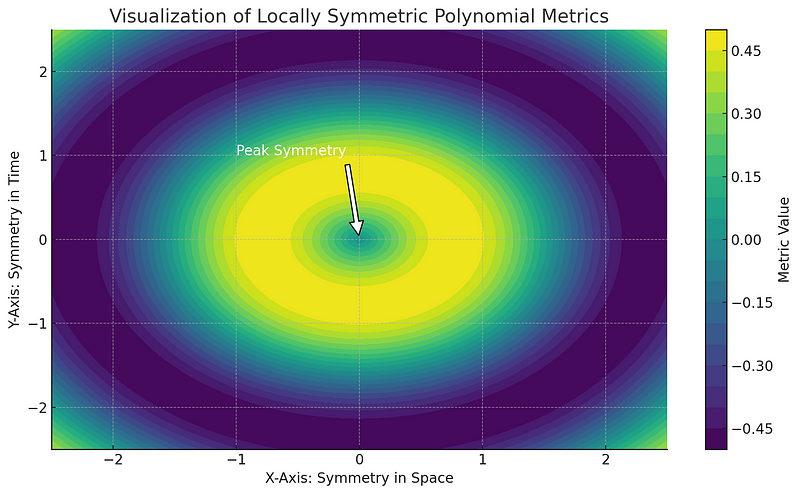
This graph illustrates the complex interplay of symmetry across space and time, beautifully captured through the mathematical elegance of locally symmetric polynomial metrics. Observe how the peaks and troughs of the graph are mirrored, exemplifying the central concept of symmetry in our exploration. The vibrant hues transition fluidly, symbolizing the continuous nature of these metrics throughout the mathematical landscape.
Chapter 2: Practical Implications and Future Directions
The investigation of locally symmetric polynomial metrics extends beyond theoretical inquiry; it is a journey into uncharted territories of knowledge. From the intricate movements of celestial bodies to the quantum phenomena within subatomic realms, these metrics provide insights into the fundamental laws that govern our universe. They possess the potential to transform our understanding of spacetime, gravitational fields, and even the enigmatic dark matter that pervades the cosmos.
Section 2.1: Shaping Tomorrow with Polynomial Metrics
Standing at the forefront of this mathematical frontier, we catch a glimpse of a future influenced by insights from locally symmetric polynomial metrics. Their applications extend far beyond theoretical physics, promising breakthroughs in cryptography, data analysis, and even artificial intelligence. By leveraging the power of symmetry, we unlock new dimensions of efficiency, security, and comprehension, paving the way for a future where mathematics illuminates the darkest corners of our universe.
Subsection 2.1.1: A New Lexicon for the Cosmos
These metrics present a fresh lexicon to articulate the curvature of space, offering a framework that could potentially unveil the secrets of the universe's architecture.
Section 2.2: Bridging Disciplines
Locally symmetric polynomial metrics act as a conduit between geometry and physics, providing insights that could transform our understanding of spacetime and gravitational phenomena.
Subsection 2.2.1: A Creative Canvas
Beyond theoretical implications, these metrics hold promise for practical innovations in technology, from enhancing cybersecurity to optimizing algorithms in artificial intelligence. They offer fertile ground for mathematical exploration, inspiring future mathematicians to expand the boundaries of knowledge.
In conclusion, as we traverse the intricate landscape of locally symmetric polynomial metrics, we are reminded of the beauty inherent in the pursuit of understanding and the quest to unveil the mysteries of our universe. This journey stands as a testament to human curiosity — a beacon of hope, illuminating the remarkable discoveries awaiting us at the frontiers of mathematics and physics. Let this exploration ignite your imagination, for within the realm of locally symmetric polynomial metrics lie not just the keys to deciphering the cosmos, but the essence of wonder and the limitless potential of the human intellect.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your insight into the future of technology. Subscribe for new videos every Saturday!