# Understanding How the Sun Produces Light Despite Low Temperatures
Written on
Chapter 1: The Sun's Temperature Dilemma
The Sun's core, which reaches temperatures of merely 15 million degrees Kelvin, seems insufficient for nuclear fusion, which typically demands around 100 million degrees. So, how does the Sun manage to emit light? The answer lies in a fascinating quantum phenomenon called quantum tunneling.
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: The Basics of Stellar Fusion
Students often learn that stars, due to their immense gravitational pull, achieve sufficient pressure and temperature to overcome the natural repulsion between protons in hydrogen atoms, allowing them to fuse into helium. This fusion process results in helium that has a slightly lower mass than the original hydrogen atoms, with the lost mass converting into a substantial amount of energy, as described by Einstein’s equation, E=mc². This equation illustrates that even a minuscule amount of mass (m) can transform into an enormous amount of energy (E) when multiplied by the speed of light squared (c²), approximately 9 x 10¹⁶ m²/s².
However, there's a significant issue: the core of the Sun does not reach the temperatures needed for nuclear fusion to take place. In contrast, fusion reactors on Earth require far higher temperatures to function.
Section 1.2: Quantum Mechanics Explained
Quantum mechanics explores the realm of the extremely small, where the conventional rules of physics become unrecognizable. In this domain, particles can seemingly appear beyond barriers that should be insurmountable, exist in a state of probability until observed, and interact instantaneously over vast distances, among other perplexing behaviors. Despite its oddities, quantum mechanics has provided invaluable insights into resolving numerous challenges in classical physics.
The foundation of quantum mechanics lies in wave-particle duality, articulated by Schrödinger’s equation. This concept posits that particles exist as a probability wave until they are detected, at which point they "choose" a specific location. While this notion may seem absurd, it has been repeatedly validated through experimentation.
Section 1.3: The Double Slit Experiment
Young’s double slit experiment famously demonstrated the principles of wave-particle duality. In this experiment, photons are directed at a barrier featuring two slits, with a detection screen positioned behind. If photons act as solid particles, they would pass through the slits, creating two distinct patterns on the screen. Conversely, if they behave as waves, they would propagate through both slits and interfere with one another, producing an intricate pattern of alternating dark and light bands.
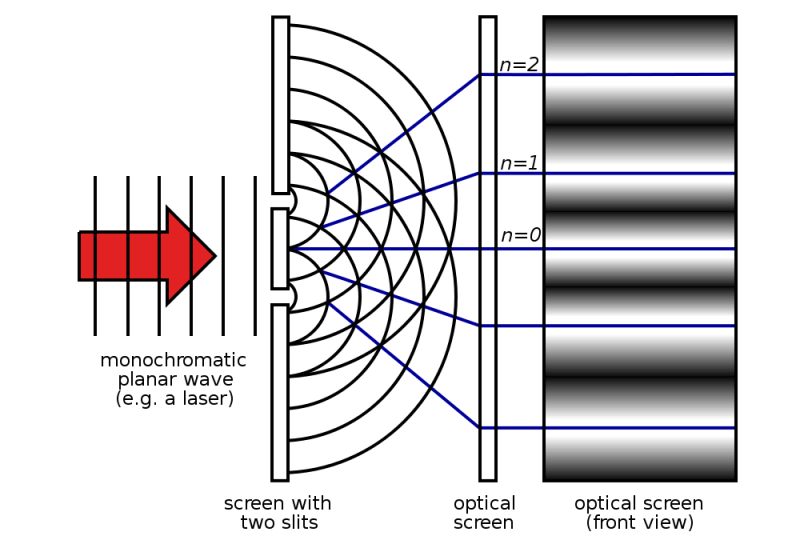
When the only measurement is the detection screen, photons exhibit a wave pattern. However, if detection occurs while passing through the slits, a particle pattern emerges. The outcome on the screen hinges entirely on whether the photons are observed while traversing the slits, forcing them to abandon their wave-like state and select a specific location.
Chapter 2: Quantum Tunneling and Its Role in Solar Fusion
So how does this relate to solar fusion? Viewing hydrogen atoms—particularly the protons in their nuclei—as solid particles implies they lack the necessary energy to approach one another closely enough for the strong nuclear force to take effect, which only operates within distances of about 10⁻¹⁵ meters. However, if we conceptualize them as probability waves, they can potentially "tunnel" through the energy barrier due to a peculiar wave phenomenon known as evanescent waves.
Section 2.1: Understanding Evanescent Waves
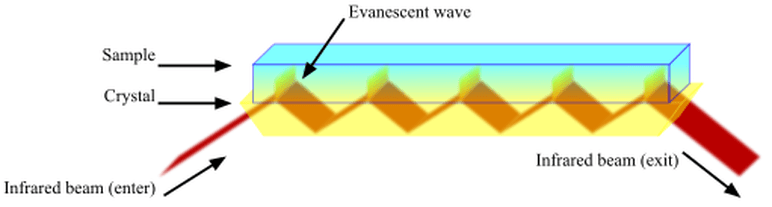
When a wave transitions from one medium to another, it undergoes reflection and refraction. For instance, directing a laser beam onto a body of water results in some light reflecting back and some penetrating the surface. The ratio of reflection to refraction is influenced by the light's angle and the mediums involved. In the case of air and water, the angle for total reflection is approximately 48.5 degrees.
However, this process is more intricate. Analyzing Maxwell’s equations reveals that when a wave strikes a new medium, a transient wave is generated, lasting only for a brief span of wavelengths. This evanescent wave can extend further under specific conditions.
Section 2.2: Quantum Tunneling in Action
Now, consider quantum particles confined in a hypothetical box. They have defined probabilities of being located in various areas within the box, along with a non-zero probability of existing outside it. This means they have a chance—albeit small—of appearing beyond barriers that should be impossible to cross.
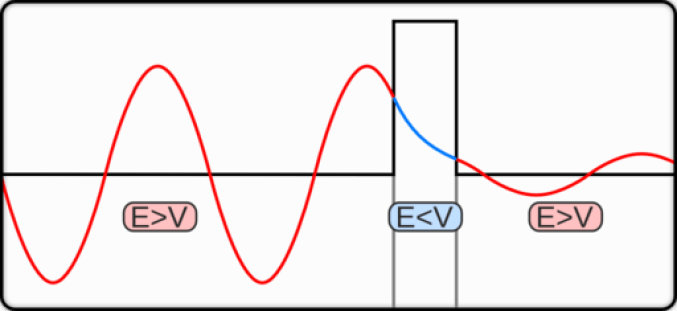
When applying this to solar fusion, the quantum particles of interest are the protons in hydrogen atoms, and the formidable energy barrier they face is the high energy required for fusion. Because they behave as probability waves, there exists a non-negligible chance that some protons will successfully tunnel through this barrier, permitting the strong nuclear force to engage and solar fusion to occur. Essentially, protons possess a slight likelihood of being found in positions that seem improbable, such as being in close proximity without sufficient energy.
Even though this concept may seem outlandish, the mathematics supports it. The Sun's core contains approximately 10⁵⁶ hydrogen atoms, and the probability of two protons fusing due to quantum tunneling is roughly 1 in 10²⁸. For the Sun to generate the energy it needs, around 3.7 x 10³⁸ fusion reactions must transpire every second. Despite the rarity of quantum tunneling, the Sun's densely packed core allows for sufficient opportunities to surpass these slim odds.
Help support independent journalism by clicking the link below. Even a few bucks can make a big difference.
Donate to The Happy Neuron
Help support The Happy Neuron by donating or sharing with your friends.
www.paypal.com
Originally published at http://thehappyneuron.com on December 17, 2020.