Understanding Statistical Distribution and Expected Value
Written on
Introduction to Statistical Distributions
Statistical distributions play a crucial role in the work of data scientists and statisticians. However, many practitioners utilize these distributions without a solid grasp of their underlying principles. Frequently, these distributions are integrated into code or machine learning models with minimal user interaction.
As a mathematician and statistician, I advocate for data scientists to cultivate a thorough understanding of the mathematical concepts they engage with. This foundational knowledge not only enhances their skills but also empowers them to adapt their methods when necessary.
In this discussion, I'll delve into a recent problem that required an understanding of probability distribution functions, how to construct them, and their relationship to concepts like probability density and expected value (often referred to as mean value). Let's begin with the problem at hand.

Analyzing the Initial Problem
The problem presents a straightforward scenario where a marksman takes n shots, all of which are guaranteed to hit the target. We define the random variable Y as the radius of the smallest circle that encompasses all the shots. To formalize this, we can define Y mathematically.
Here’s a diagram showing the scenario, where the marksman's shots are represented by red crosses, and a dotted circle with radius y illustrates the smallest circle enclosing all the shots:
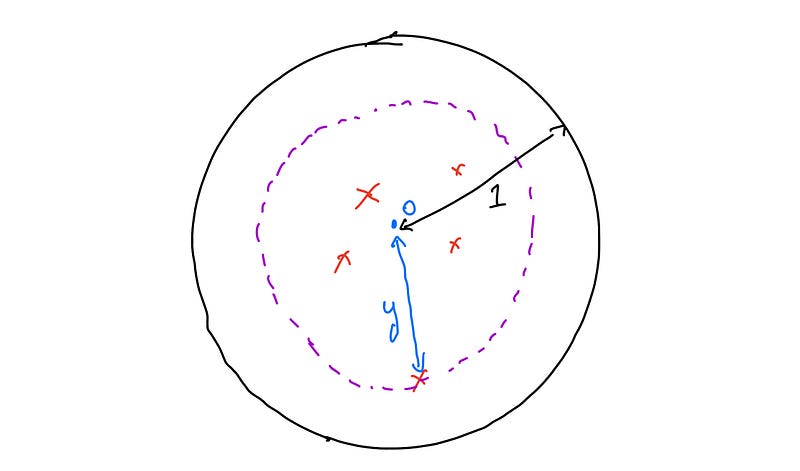
To find the total probability that our random variable Y is less than or equal to y, we note that all n shots must land within a distance y from the origin O. Each shot has a probability of landing within distance t as t². Therefore, the probability that all n shots fall within distance y is:
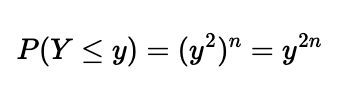
Having established a function that defines the total probability of our random variable Y being less than a specified value, we recognize this as a cumulative distribution function (CDF). For those familiar with basic statistics, the probability density function (PDF) of a random variable is derived from its CDF. In simpler terms, the PDF indicates the probability that the value of the random variable equals a specific value. To obtain the PDF P(Y = y), we differentiate the CDF:
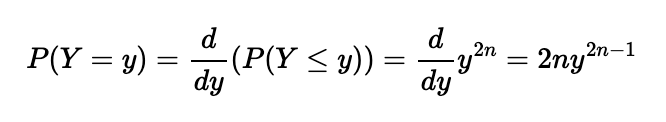
Next, we need to calculate the expected value of the area of the circle defined by the random variable Y. In cases with discrete variables, the mean is the sum of the values multiplied by their respective probabilities. The expected value extends this concept to continuous variables. The formula for the expected value of a continuous random variable is:
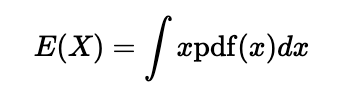
In this instance, the random variable X represents the area of the circle with radius Y. For any radius y, the area is given by πy², and the corresponding probability is defined by our PDF. Considering that our radius can range from 0 to 1, we can express this as:
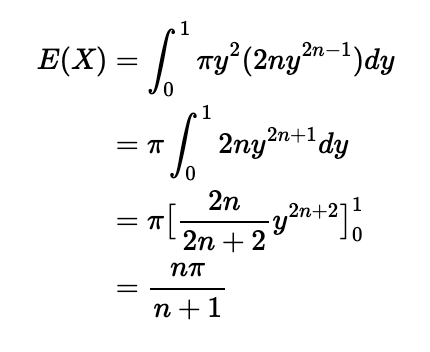
Exploring the Second Part of the Problem
The second part of the problem introduces a new complexity: the random variable now accounts for the elimination of the shot that is the farthest from O. To determine the PDF of this new variable—let's denote it as Z—we can apply a similar approach as before.
We begin by deriving the CDF of Z, aiming to differentiate it to obtain the PDF. For a given radius z, the scenarios where our random variable Z is less than or equal to z can be outlined as follows:
- All n shots fall within a radius of z. Even if the farthest shot is removed, the remaining n-1 shots will still be within the radius.
- All but one of the n shots fall within a radius of z, with one shot falling outside. Any of the shots could be the one that misses, leading to n possible outcomes.
Thus, we can establish the CDF of Z as:
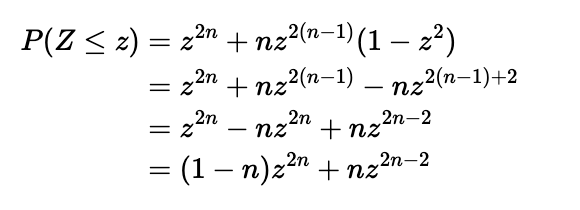
Differentiating this function allows us to derive the PDF of Z:
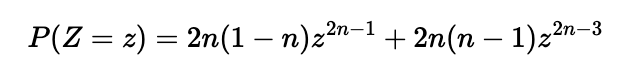
Finally, we can compute the expected value of the radius of the circle defined by the random variable Z as follows:
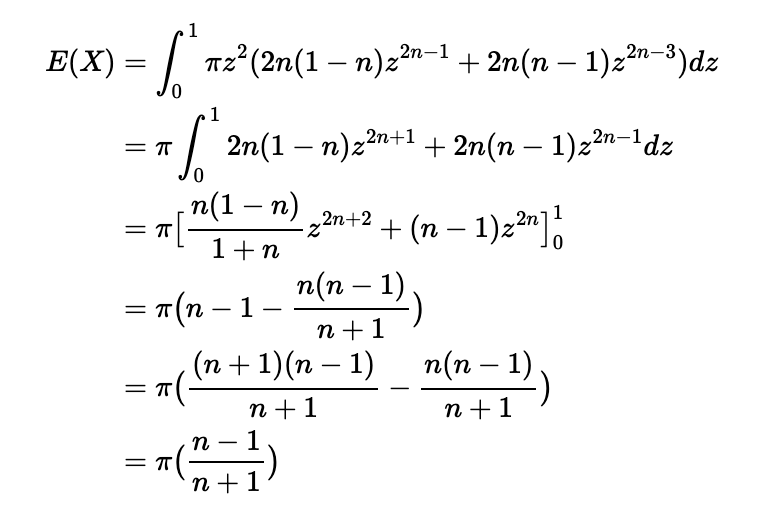
Conclusion
What are your thoughts on this problem and its resolution? I invite you to share your insights!