Chapter 1: Introduction to the Pseudo-Inverse

The pseudo-inverse, often referred to as the Moore-Penrose inverse, is a vital concept in linear algebra that extends the idea of matrix inversion to cases where matrices are not invertible. This mathematical tool has wide-ranging applications across various fields such as science, engineering, and data analysis.

Understanding the Concept

To grasp the essence of the pseudo-inverse, one can visualize it geometrically. Consider a matrix A that does not have full rank, meaning its columns fail to span the entire vector space. The pseudo-inverse of A can be viewed as projecting a vector b onto the column space of A, followed by a "back projection" onto the complete vector space. This results in a vector that is the "closest" to b yet lies within the column space of A. Below is a simple example using Python's NumPy library:

import numpy as np

A = np.array([[2, 2], [4, 6], [4, 10]]) # Define matrix A

b = np.array([1, 2, 4]) # Define vector b

U, S, V = np.linalg.svd(A, full_matrices=False) # Compute SVD of A

Sinv = np.diag(1/S) # Calculate reciprocal of singular values

Aplus = V.T @ Sinv @ U.T # Compute pseudo-inverse of A

x = Aplus @ b # Solve for x in Ax = b

print("U =n", np.round(U, 2))

print("S =n", np.round(S, 2))

print("V =n", np.round(V, 2))

print("Sinv =n", np.round(Sinv, 2))

print("Aplus =n", np.round(Aplus, 2))

print("x =n", np.round(x, 2))

Properties of the Pseudo-Inverse

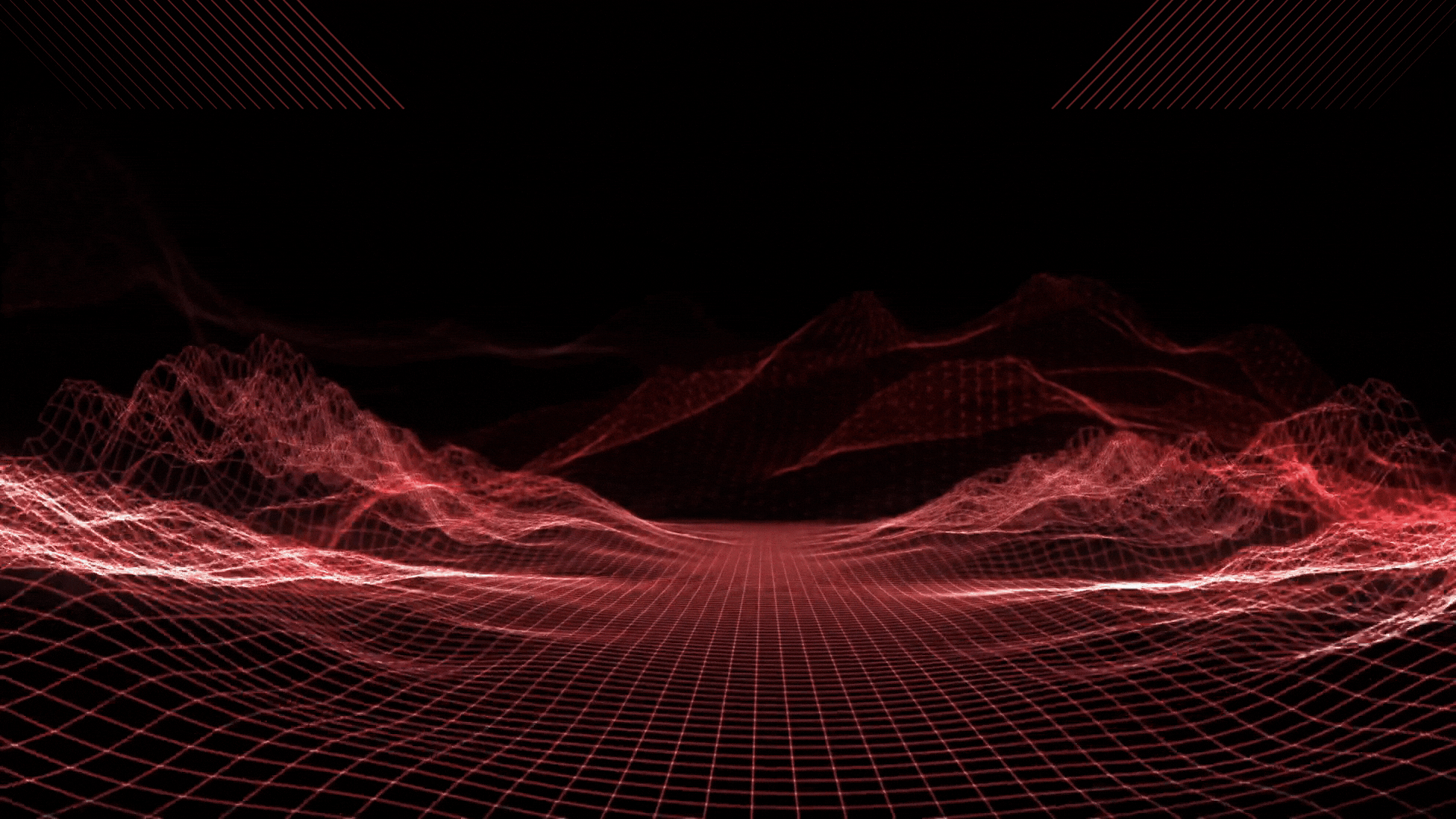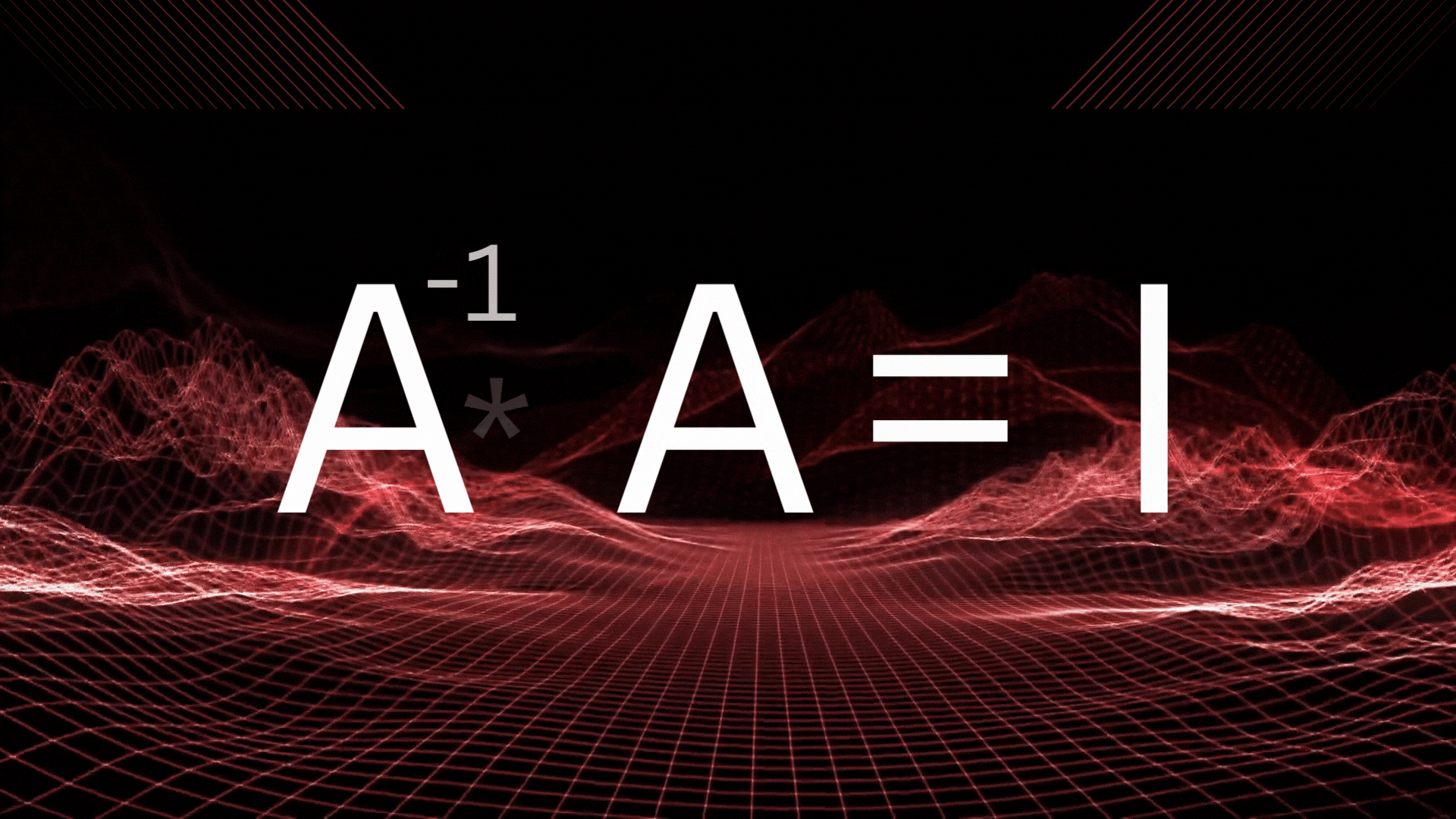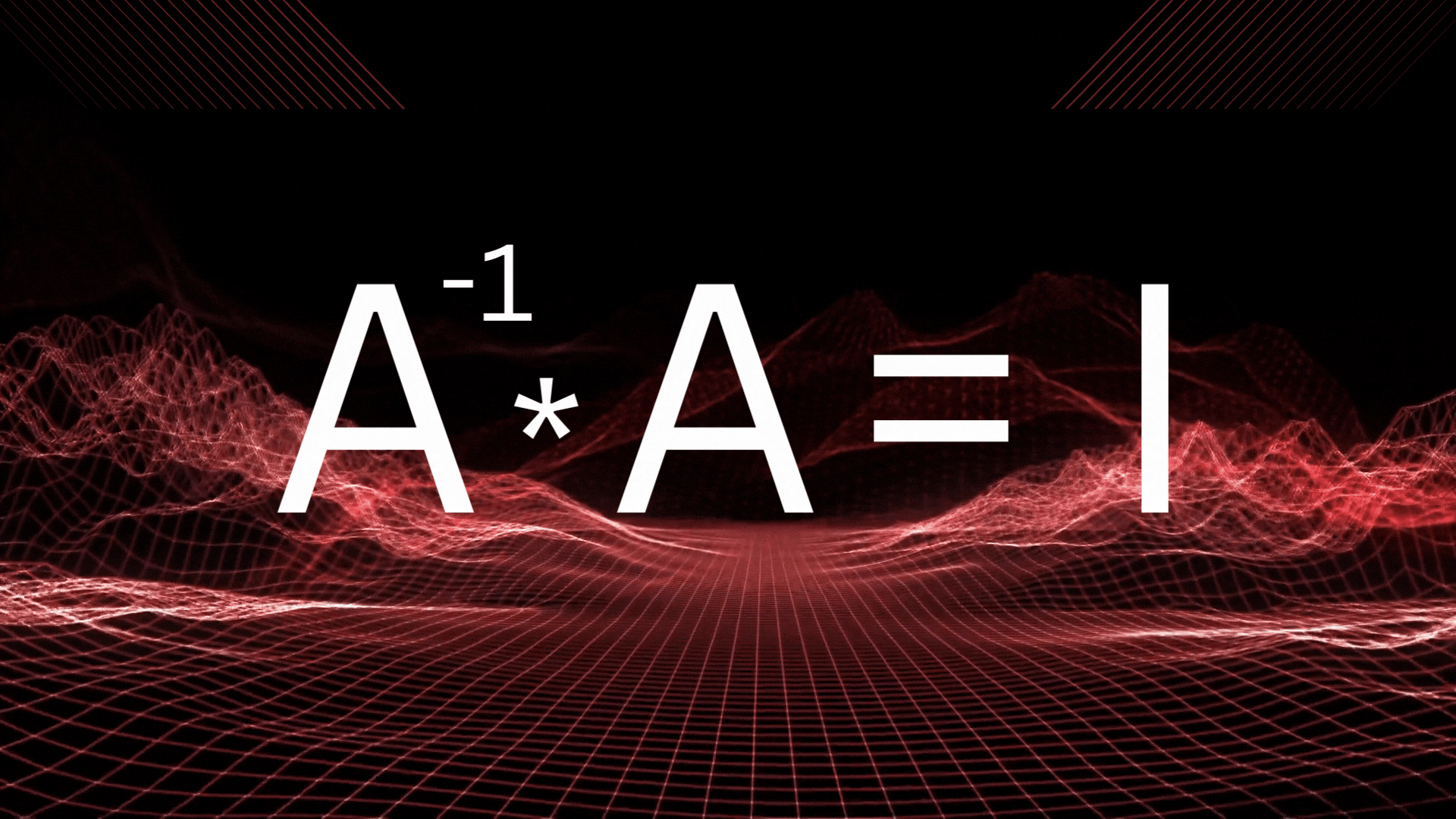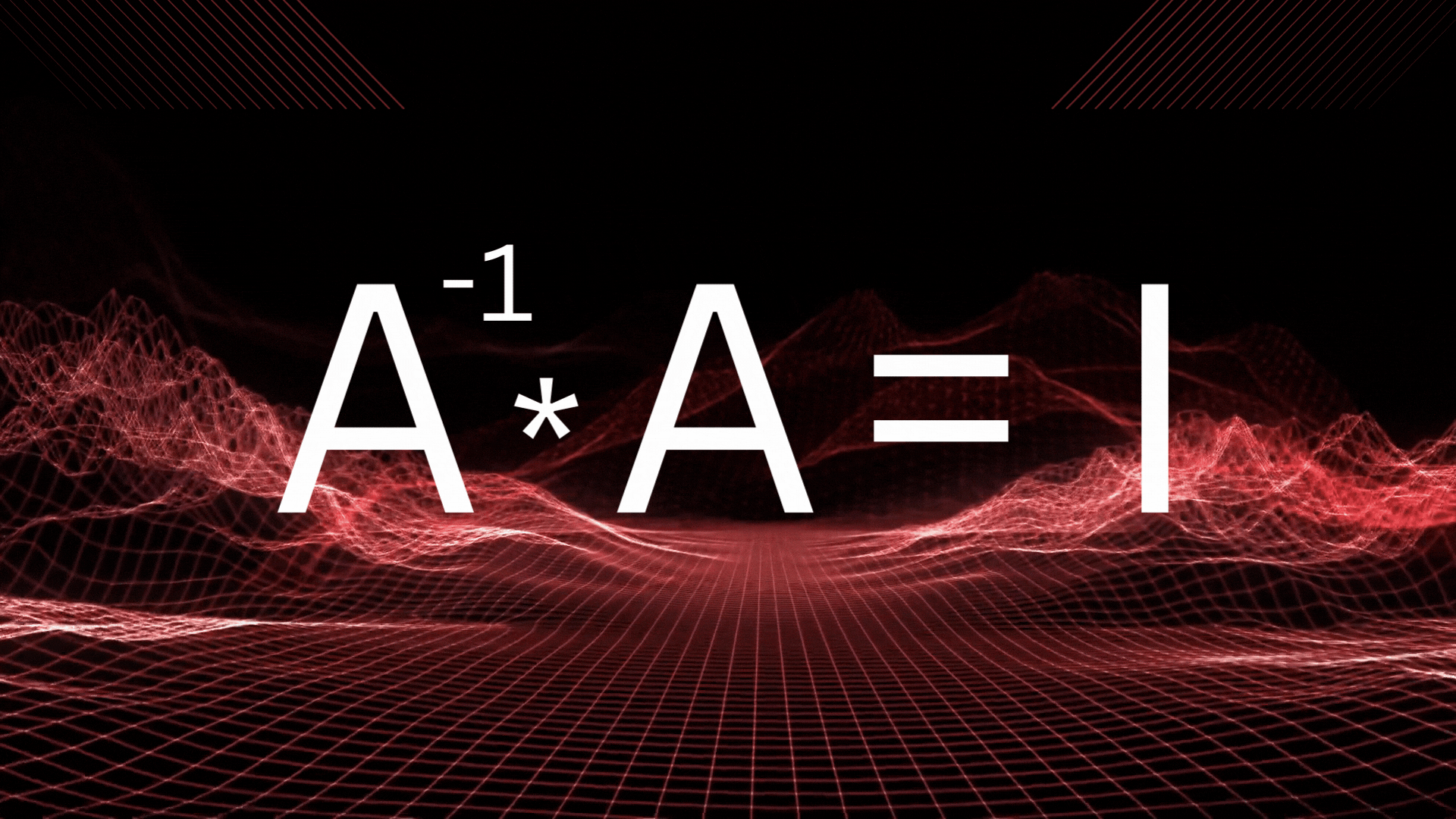
The pseudo-inverse of a matrix A is denoted as A?. It satisfies several essential mathematical properties:

1. A * A? * A = A
2. A? * A * A? = A?
3. (A * A?)^T = A * A?
4. (A? * A)^T = A? * A

Thus, the matrices A?A and AA? are projection matrices, which means they are symmetric, idempotent, and have a rank corresponding to the number of linearly independent rows or columns of A.

The pseudo-inverse is particularly valuable in minimizing the distance ||Ax — b||, where the solution is given by x = A?b.

General Properties

• The pseudo-inverse always exists, even for non-invertible matrices.
• It is unique.
• The pseudo-inverse of a product of matrices can be computed by reversing the order of their pseudo-inverses: (AB)? = B?A?.
• It provides the minimum norm solution for underdetermined systems of equations.
• It is crucial for resolving least-squares problems, which aim to find a solution that minimizes the squared errors.

Practical Applications

1. Solving Linear Systems: The pseudo-inverse is instrumental in solving equations without exact solutions.
2. Data Compression: It approximates matrices with lower-rank matrices through singular value decomposition (SVD).
3. Image Processing: It aids in restoring degraded images or recovering lost information.
4. Control Theory: It helps in controlling robotic systems and other applications requiring optimal solutions.
5. Machine Learning: Techniques such as linear regression, principal component analysis, and support vector machines utilize the pseudo-inverse.

Chapter 2: Applications of the Pseudo-Inverse

The video "Advanced Linear Algebra - Lecture 38: Introduction to the Pseudoinverse" provides an in-depth exploration of the pseudo-inverse, discussing its theoretical foundation and practical implications.

The video "Introduction to the Pseudo-Inverse" serves as a primer on the concept, offering clear examples and applications relevant to data science and engineering.

Solving Linear Systems of Equations

One of the most significant uses of the pseudo-inverse is in resolving linear equations that do not have a precise solution. In real-world scenarios, it's common to encounter underdetermined or overdetermined systems. In underdetermined systems, where there are more variables than equations, the pseudo-inverse can yield a solution that minimizes the distance to the target vector.

For instance, take the equations:

3x + 2y = 5

2x + 3y = 7

This system can be solved as follows:

import numpy as np

A = np.array([[3, 2], [2, 3]])

b = np.array([5, 7])

A_pinv = np.linalg.pinv(A)

x = np.dot(A_pinv, b)

Data Compression Techniques

The pseudo-inverse also plays a crucial role in data compression by approximating matrices with lower-rank versions. This involves computing the singular value decomposition (SVD) and truncating it by retaining only the most significant singular values and vectors.

For example, consider an image represented as a matrix A of size m x n:

U, s, V = np.linalg.svd(A)

A_k = U[:, :k] @ np.diag(s[:k]) @ V[:k, :]

A_k_pinv = np.linalg.pinv(A_k)

A_reconstructed = A_k_pinv @ A_k

Conclusion

In summary, the pseudo-inverse is a robust mathematical tool with extensive applications in diverse fields, including science, engineering, and data analysis. Its ability to handle non-invertible matrices and provide solutions to complex linear systems makes it indispensable in modern computational techniques.

For more insightful content, consider exploring additional resources on related topics.