Chapter 1: The Gender Bias Dilemma

Did the University of California, Berkeley, exhibit gender bias in its admission process back in 1973? If you scrutinize the statistics, you might conclude there was indeed bias. The catch? Depending on the data you examine, the apparent bias may favor a different gender.

This may sound perplexing, but rest assured, it’s a compelling example of the importance of careful interpretation when presented with seemingly indisputable statistics. The way data is presented can significantly influence perceptions, and this isn’t necessarily due to manipulation. Instead, it often arises from the selection of specific figures which can yield contradictory results, even when all data is accurate.

As Winston Churchill famously suggested, "Never trust a statistic if you haven’t falsified it yourself." A more fitting adaptation might be, "Never trust a statistic if you’re unaware of all the figures."

Let’s delve deeper into this issue and explore one of the most renowned paradoxes in statistical history: Simpson's Paradox, also referred to as the Yule-Simpson effect, amalgamation paradox, or reversal paradox.

Key Facts to Consider

1. In 1973, the overall acceptance rate for female applicants at UC Berkeley across four departments was approximately 30%, while the rate for male applicants was about 47%.
2. Within each department, however, female applicants had a higher acceptance rate than their male counterparts.

This presents a contradiction: Fact 1 suggests that men were favored, while Fact 2 indicates a preference for women. Which interpretation is accurate? To clarify this, we need to analyze the data.

Examining the Data for Fact 1

The data appears straightforward; the acceptance rate is calculated by dividing the number of accepted applicants by the total number of applicants. The resulting percentage for men is notably higher than for women, confirming Fact 1.

Investigating the Data for Fact 2

We’ll focus on four departments, which we’ll label as Departments 1, 2, 3, and 4. Let's review the data for Department 1.

Here, we observe that the acceptance rate for males is significantly lower than for females, yet male applications outnumber female applications.

Now, let’s examine Department 2.

Similar trends appear; the male acceptance rate is less than that of females, although the disparity is less pronounced. Again, more men applied than women.

What about Department 3?

Once more, male acceptance rates fall short of female rates, but the difference in applications is less significant this time.

Lastly, let’s look at Department 4.

Again, the acceptance rate for women surpasses that of men, and the application numbers are comparable.

Thus, both facts are indeed accurate. Although the overall acceptance rate for women is lower than for men, each department shows a higher acceptance rate for women. How can this be?

Clarifying the Numbers

This scenario appears contradictory. The overall acceptance rate for women is lower, while department-specific rates favor them. To visualize this, let's examine the percentages.

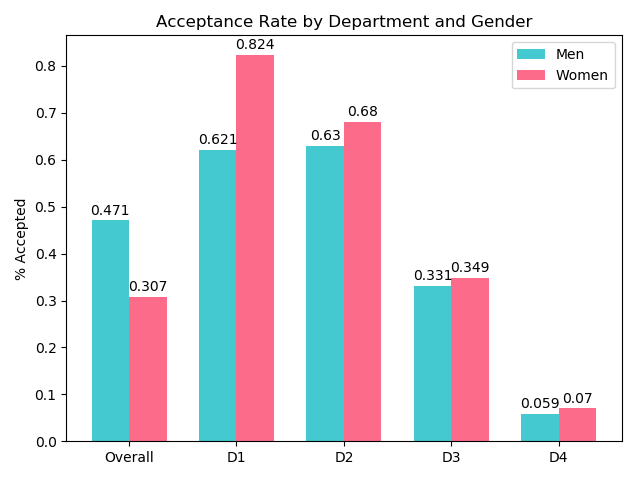
Now, let’s shift our focus to total application numbers rather than percentages.

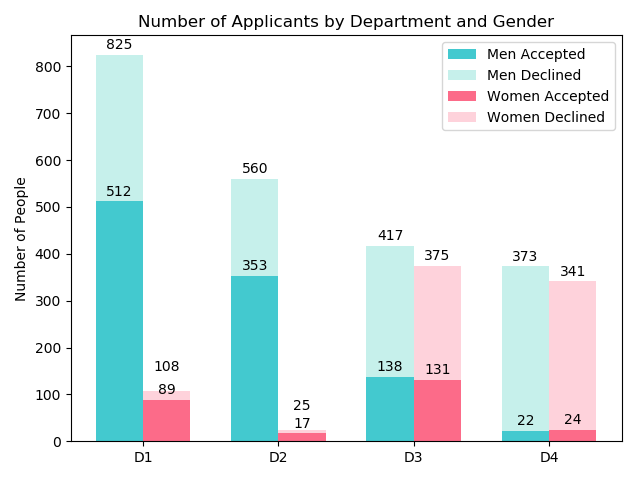
In this representation, we notice that Department 1 accepted both a high number and percentage of applicants, yet very few women applied. The same pattern is observed in Department 2. In Departments 3 and 4, application numbers are nearly equal, but overall acceptance rates are lower compared to the other departments.

This disparity explains why women’s overall acceptance rate is lower: they applied more frequently to competitive departments with stringent admission criteria. Hence, the conflicting statistics are clarified.

Simpson's Paradox Illustrated Through Sports

Another way to illustrate Simpson's Paradox is through a sports analogy. Imagine two athletes, Lisa and Bart, competing in a 10-mile event. Bart swims 1 mile and runs 9 miles, while Lisa swims 6 miles and runs 4 miles. Despite being faster in both swimming and running, Lisa takes longer to complete the race than Bart due to the distance she swims.

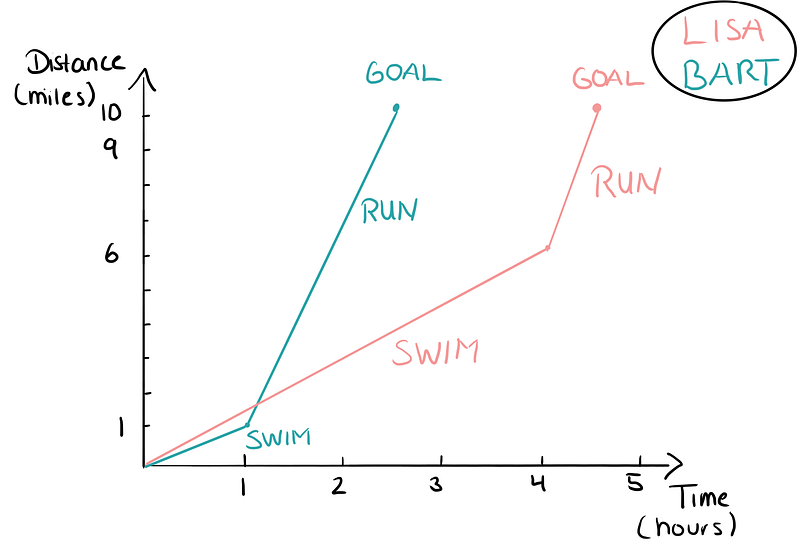
This scenario is reminiscent of the UC Berkeley admissions: women were competing in more challenging departments, akin to swimming longer distances, while men faced less stringent criteria, paralleling running shorter distances.

Conclusion

In addressing the initial query: No, the data does not definitively suggest discrimination against women, nor does it imply bias against men. However, this doesn’t conclusively rule out the presence of bias. The determination of bias requires a qualitative analysis beyond mere statistical examination, a task best suited for social scientists rather than mathematicians or data scientists.

Exploring the Data Further

The dataset for this analysis can be accessed through various sources, including the R Programming Language. By entering data(USBAdmissions) in your R console, you can explore the dataset. Note that two departments (Departments C and E) were intentionally omitted to highlight Simpson's Paradox. The visualizations were generated using Python's Matplotlib. I encourage you to download the dataset and conduct your own analysis to deepen your understanding of Simpson's Paradox.

Enjoy your data exploration!

This video titled "Are University Admissions Biased? | Simpson's Paradox Part 2" delves into the intricacies of admission biases, particularly focusing on the Simpson's Paradox.

The video "[Quick guide] Simpson's paradox explained: UC Berkeley, 1973 - Gender bias? (Part 2)" provides a concise explanation of how Simpson's Paradox manifests in the context of gender bias in university admissions.