Chapter 1: Introduction to the Puzzle

Welcome to the fourth installment of our tricky logic puzzle series! In this challenge, we introduce "Cheat," the robot. As depicted in the title image, there is a sequence of five light bulbs that are currently illuminated. Cheat provides the following information:

With this initial scenario, your task is to determine a configuration for the light bulbs (on-off) that meets these criteria:

1. An even number of bulbs must be lit.
2. Cheat is not telling the truth.
3. Each illuminated bulb must be adjacent to at least one other that is also lit.
4. The fourth bulb from the left must be turned off.

Remember, in this puzzle, all liars consistently lie. The final configuration of the light bulbs must adhere to all of these stipulations. Think you can crack it?

Spoiler Alert

If you prefer to solve this puzzle on your own, I recommend stopping here. The following sections will reveal the solution, so you can compare your reasoning afterward.

Chapter 2: Analyzing the Puzzle — Narrowing Down Options

The key to solving this puzzle is to focus on eliminating possibilities rather than seeking the final arrangement right away. By examining the list of conditions, you’ll notice that the fourth point provides a definitive answer: the fourth bulb must be off.

This leads us to the following initial configuration:

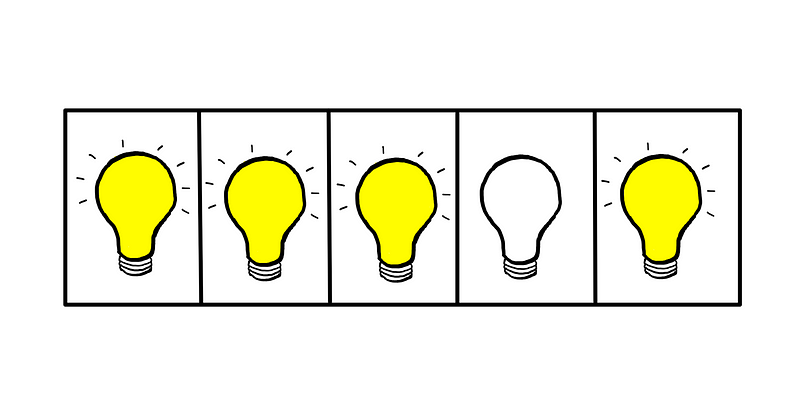
Next, let’s assess this setup against our conditions:

1. An even number of bulbs are lit — Satisfied.
2. Cheat is lying — Satisfied.
3. Each lit bulb is adjacent to another lit bulb — NOT satisfied.
4. The fourth bulb from the left is off — Satisfied.

Condition 3 is not met since the rightmost bulb lacks an adjacent lit bulb. To resolve this, we can turn off the rightmost light bulb:

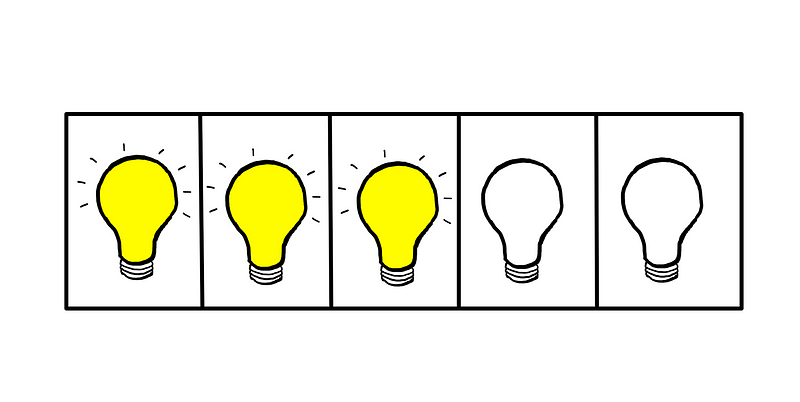
Now, we find ourselves with an odd number of bulbs lit, and Cheat's original statement holds true because the two switched-off bulbs are adjacent:

1. An even number of bulbs are lit — NOT satisfied.
2. Cheat is lying — Not satisfied.
3. Each lit bulb is adjacent to another lit bulb — Satisfied.
4. The fourth bulb from the left is off — Satisfied.

Although it may not seem evident, we are nearing a solution. Let’s delve into our final considerations.

Chapter 3: Unveiling the Solution to the Puzzle

If we switch off one more bulb, we can achieve an even number of illuminated bulbs again. The question is: which one should we turn off? Examining Cheat's statement will guide us.

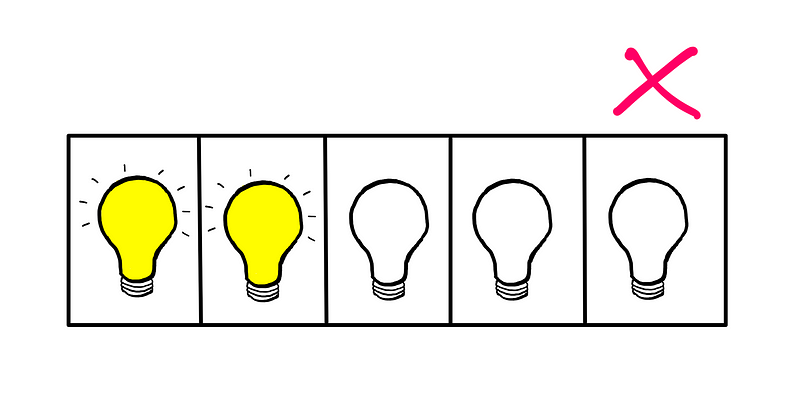
If we decide to turn off the third bulb from the left, we will end up with all turned-off bulbs being adjacent, which would contradict Cheat’s lie. Therefore, the third bulb cannot be the one we switch off.

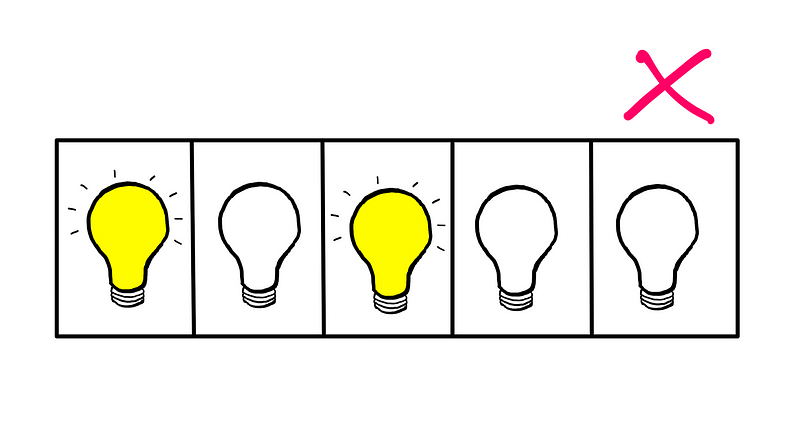
Turning off the second bulb from the left poses a problem, as both the first and third bulbs would not have adjacent lit bulbs, violating our third condition.

Ultimately, the only viable option is to turn off the first bulb. This configuration satisfies all conditions:

1. An even number of bulbs are lit — Satisfied.
2. Cheat is lying — Satisfied.
3. Each lit bulb is adjacent to another lit bulb — Satisfied.
4. The fourth bulb from the left is off — Satisfied.

If we were to turn off one more bulb, we would again have an odd number lit. Additionally, turning off both bulbs would make Cheat’s statement true once more.

Consequently, the arrangement we’ve found is the only unique solution to this puzzle. I hope you enjoyed tackling this logic challenge. Stay tuned for more puzzles in this ongoing series!

If you’re interested in exploring my complete works, check out the MAP on my about page. For those wishing to support future content, consider contributing on Patreon.

You can read the original essay here.