Chapter 1: Introduction to Tropical Geometry

Tropical geometry, a relatively recent branch of algebraic geometry, offers a unique framework for analyzing various real-world phenomena, ranging from biological systems to transportation networks. This area of study emerged in the 1990s, thanks to mathematicians like Grigory Mikhalkin, who observed that specific challenges in algebraic geometry could be simplified using a novel “tropical” arithmetic approach.

In tropical geometry, traditional arithmetic operations such as addition and multiplication are substituted with tropical operations: the minimum and addition.

For instance, in tropical arithmetic, the expression 3 ? 5 is evaluated as min{3,5} = 3. Similarly, the multiplication of two numbers a and b is interpreted as their sum:

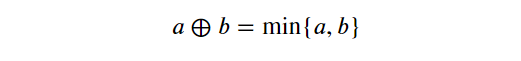
This leads us to the conclusion that 3 ? 5 = 3 + 5 = 8. A significant aspect of tropical arithmetic is its adherence to many algebraic properties found in standard arithmetic, including associativity and distributivity. For example, the following properties hold true for all numbers a, b, and c:

Associativity:

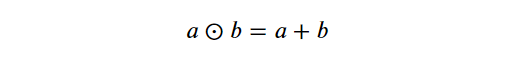
Distributivity:

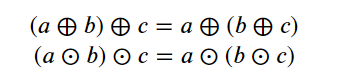
This leads to the formation of tropical semirings, which are defined by these tropical operations and exhibit their own distinct algebraic properties.

Section 1.1: The Connection to Algebraic Geometry

Tropical geometry maintains a close relationship with algebraic geometry, which investigates geometric objects defined by algebraic equations. It serves as a means to explore the combinatorial and tropical elements of algebraic geometry, such as the geometry of algebraic curves and surfaces.

One core concept of tropical geometry is that tropical varieties—specific piecewise-linear constructs—can serve to approximate algebraic varieties, which are geometric entities derived from algebraic equations. In this framework, tropical varieties are analyzed using the tropical operations of minimum and addition, rather than conventional arithmetic operations.

Subsection 1.1.1: Constructing Tropical Curves

For example, a tropical curve represents a piecewise-linear curve that approximates an algebraic curve. To create a tropical curve, one begins with an algebraic curve, substituting the usual arithmetic operations with tropical ones.

Consider the algebraic curve defined by the equation x² = x³ + 2x² + x. This smooth curve, known as an elliptic curve, can be approximated by constructing a corresponding tropical curve. This is done by rewriting the equation as x² = x(x + 1)(x + 1), allowing us to replace every addition with minimum and every multiplication with addition.

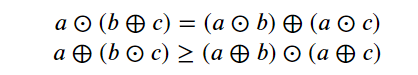
Chapter 2: Applications of Tropical Geometry

The first video titled What is tropical geometry? provides an insightful overview of the field, explaining its fundamental concepts and applications.

The second video, An introduction to tropical geometry: theory and applications (Lecture 1), delves deeper into the theoretical aspects and practical uses of tropical geometry.

Tropical geometry plays a vital role in various domains, including computer science, biology, and economics. For instance, it aids in analyzing genetic networks, which are intricate systems of interrelated genes that influence the behavior of living organisms. Additionally, tropical geometry is instrumental in examining transportation networks, such as road and rail systems, and in developing efficient algorithms for optimizing routes and minimizing transportation costs.

Conclusion

In conclusion, tropical geometry is a compelling and emerging branch of mathematics that provides a robust framework for understanding real-world phenomena. By substituting traditional arithmetic with tropical arithmetic, it enables the examination of piecewise-linear objects and serves as a valuable tool for analyzing the properties of complex systems across diverse fields.