Chapter 1: Introduction to Fractional Calculus

Welcome back to our exploration of fractional calculus! If you’ve followed along from Parts 1 and 2, you’ll be familiar with the Riemann-Liouville (R-L) fractional derivative of order ? ranging from 0 to 1.

Section 1.1: Understanding the Riemann-Liouville Derivative

As mentioned in part 2, the Riemann-Liouville operator can be viewed as the derivative of a fractional integral of order 1-?. To determine the order of the derivative, we can analyze the operator d/dt, which adds 1 to the derivative order, while the fractional integral effectively subtracts (1-?) from the total derivatives. Therefore, the order of the derivative turns out to be 1 - (1-?) = ?.

A question that often arises is whether there exists an alternative definition for the fractional derivative. The answer is yes, but it’s essential to approach this with caution. In the broader context, various operators and their properties will define distinct types of calculus. While we are acquainted with classical calculus and its derivatives, there are indeed alternative analytical approaches!

Section 1.2: The Caputo Fractional Derivative

Shifting our focus, let’s examine the Caputo fractional derivative of order ? from 0 to 1, which is defined as:

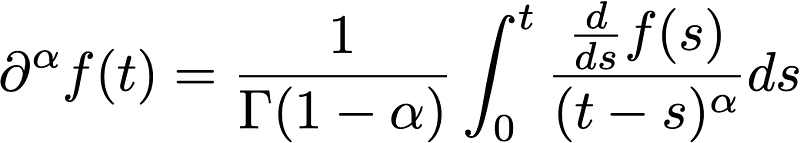
The appearance of this derivative is quite similar to its Riemann-Liouville counterpart, but the placement of the derivative within the integral makes a significant difference. One critical distinction is the requirements for the function f to ensure that each derivative is well-defined. Understanding these definitions is often half the challenge in mathematics.

For example, the Caputo derivative requires that the derivative of f be integrable. A suitable space for this is the class of strongly differentiable functions, denoted as ?¹(0,t), where the derivatives of f remain continuous and thus integrable.

However, this space may be excessively restrictive in practice. Personally, I advocate for considering broader function spaces, like the absolutely continuous functions AC[0,t]. This space is related to the Sobolev space with integrable weak derivatives, which we can delve into in future discussions.

A Practical Example

Now that we have defined both derivatives, you might wonder how different operators yield distinct calculi. Let’s explore the fractional derivatives of the function f = 1. First, we consider the Riemann-Liouville derivative:

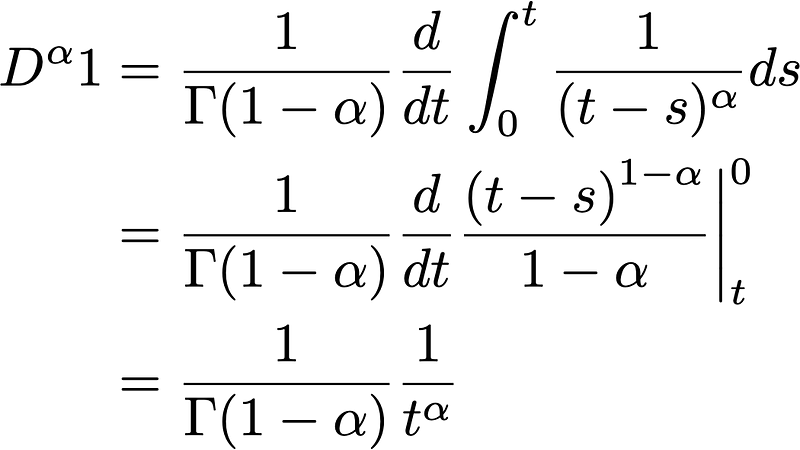
An interesting observation is that when we take the derivative of the constant function 1, we end up with a non-constant function in t! In contrast, for the Caputo derivative of the constant function 1:

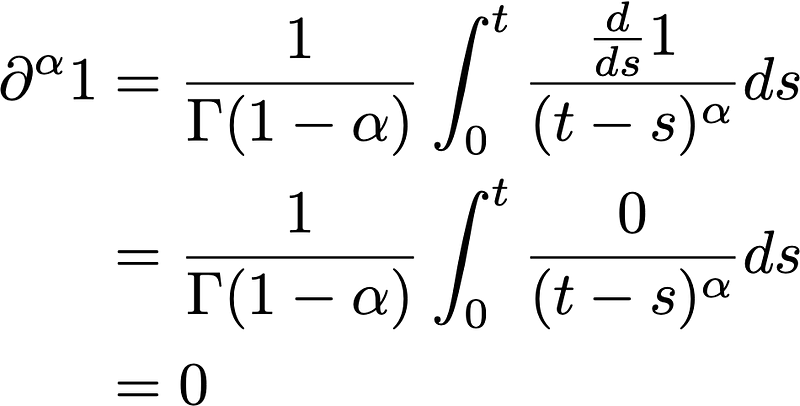
Here, everything simplifies to zero. Thus, it’s evident that these operators are not equivalent. A natural question arises: if they are not the same, which one is superior? The term "better" is somewhat ambiguous.

The fractional derivatives we’ve discussed are not uniquely defined. I believe this lack of uniqueness does not hinder the field's development; rather, it encourages an operator selection based on specific applications.

For instance, in mathematical physics and partial differential equations, one appealing aspect of the Caputo derivative is that it yields zero for the derivative of constant functions. This characteristic is crucial since time-independent solutions to partial differential equations remain unchanged over time, which is vital for the physical intuition required in applications.

Chapter 2: The Fractional Calculus Wishlist

You might wonder: with so many operators, are there any established guidelines we should follow? While the rules are not entirely rigid, Hilfer and Luchko proposed a set of guidelines that seem quite relevant. In their paper, they outline the "fractional calculus wishlist," which includes the following:

1. Fractional derivatives and integrals should function as linear operators acting on linear spaces, akin to how matrices transform vectors in linear algebra.
2. The composition of fractional integrals of different orders should yield the fractional integral of the sum of those orders. For example, applying a half-integral twice should produce a full integral.
3. The fractional derivative of a fractional integral should recover the original function, resembling the fundamental theorem of calculus.
4. As the order of the derivative approaches 1, we should retrieve the classical derivative and identity operator to align with traditional derivative theory.

Additionally, as the order approaches 1, we would hope to regain a Leibniz Rule (Product Rule). Although fractional derivative operators do not possess a neat product rule, we wish to recover the classical one in limiting cases.

By paying special attention to the domains of our operators, we can define the two derivatives we have analyzed to satisfy this wishlist. There are other derivatives of interest, such as the Hilfer and Riesz derivatives, which we can explore in future discussions.

Let’s continue our journey into the fascinating realm of fractional calculus and its wide-ranging applications! I hope you found this introductory overview engaging!

Feel free to share your thoughts in the comments below! Your support through claps and follows is greatly appreciated as it helps me grow and ensures that you enjoy this type of content. I eagerly anticipate sharing more articles with you!