Challenging My Limits: Insights from the 2024 China Math Olympiad
Written on
Chapter 1: Navigating Complex Problems
The efficiency of China’s educational system is impressive, as evidenced by the fact that their 2024 National Math Olympiad was held as early as November 2023.
I enjoy pushing my own boundaries with these mathematical challenges. It’s not solely about the thrill of solving a problem, but also about experiencing the confusion that my students feel when they encounter complex concepts.
Here’s how my thought process unfolded...
Section 1.1: The Initial Encounter
I took my time reading the problem twice, yet it remained elusive. To clarify my understanding, I decided to experiment with smaller values of n, starting with n = 2. I aimed to find x1 and x2 such that:
2 = (x1)(x2)...(x2023).
However, I quickly realized that with n = 2, I only had x1 and x2. This raised a critical question: what about x3 through x2023? Does this imply that n must exceed 2023? The problem states “all n ∈ N,” yet I was torn between needing to include all terms or simply focusing on x1 and x2. If I only considered x1 and x2, I could set x1 = 1 and x2 = 2. It dawned on me that 2 is prime — leading me to believe the smallest value for ? should be 1, given both x1 and x2 are less than 2 (although, on reflection, the true minimum ? is 0).
I proceeded to explore cases for n = 3 and n = 4, but the confusion persisted.
Subsection 1.1.1: The Growing Doubts
I was uncertain whether x1 through x2023 needed to be distinct values. My instinct suggested they should be distinct for the problem to hold meaning, yet there was no stipulation in the problem itself. I felt like I was missing key information and even doubted the clarity of the problem statement, wondering if something had been lost in translation.
Section 1.2: Seeking Clarity
At this point, I turned to the solutions available on Art of Problem Solving. After reviewing several responses, I began to grasp the mathematics behind the problem and pinpoint where I had faltered.
The key was to consider much larger values of n — specifically, numbers that possess more than 2023 factors.
For instance, if we let n = 2²?²?, we seek factors x1, x2,..., x2023 such that:
2²?²? = (x1)(x2)...(x2023), ensuring each factor is either prime or as minimal as possible.
What strategy would you adopt? To minimize the non-prime factor, an optimal approach would involve setting x1 = x2 = ... = x2022 = 2, with x2023 = 2², thus achieving the necessary 2024 prime factors of 2. Consequently, the smallest value for ? becomes 1/1012, since n = 2²?²? and 2 = 2024 / 1012.
Chapter 2: Expanding the Horizons
Video Description: Explore how the simplest problem from one of the toughest math Olympiads can be perplexing yet enlightening.
The second video title is China Math Olympiad Problem That Is Very Difficult.
Video Description: Discover the complexities of a challenging math Olympiad problem that will test your analytical skills.
What happens when n increases? For example, with n = 3²?²?, the method remains similar — you’d find that ? is still 1/1012.
Consider the case with diverse prime factors, such as n = 2 × 3 × 5 × 7... up to the 2024th prime. Clearly, not all 2023 factors can be prime (since n has 2024 prime factors). Therefore, a wise approach would be to set x1 = 2 × 3, with the remaining x2 through x2023 as prime.
The calculation for ? becomes more complicated, but solving (2 × 3) = n^? leads us to conclude that ? = log?(2 × 3). This value of ? is significantly lower than the 1/1012 we derived using 2024 repeated prime factors.
I convinced myself by comparing scenarios involving four different prime factors versus those with four repeated prime factors.
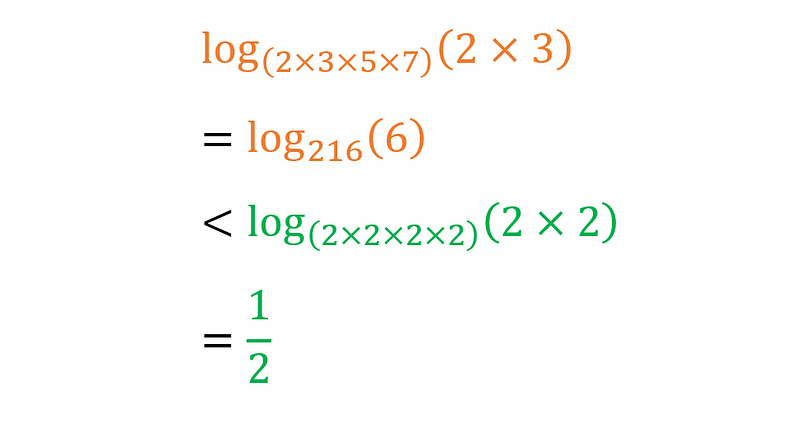
Ultimately, to discover the smallest value of ? applicable for all n, it becomes logical that 1/1012 would be the answer.
Proof of Concept
The example of n = 2²?²? illustrates that ? ≥ 1/1012 (as this scenario eliminates any smaller values of ?).
The challenging aspect is proving that ? ≤ 1/1012. Among the various proofs I encountered, my favorite was the proof by induction, which establishes a broader result: it is always feasible to decompose any n into k factors, where each factor is either prime or does not exceed ? = 2/(k+1). Our specific problem is a unique case where k = 2023, yielding the solution of ? = 2/2024 = 1/1012.
I find the concept of induction on k, the number of required factors, to be quite appealing. Not only does it allow for a general proof, but it also resonates intuitively — utilizing the smallest primes to form the largest factor possible (without breaching the upper limit). The remaining primes can then be allocated into (k - 1) factors that also remain sufficiently small, as indicated by the inductive hypothesis.
Simple, right?
Of course, I’m being facetious. I doubt I would have arrived at this solution even after hours of contemplation. Nevertheless, I would have made progress if I had set aside the misconception that the x1, x2,..., x2023 needed to be distinct. My initial confusion regarding small values of n could have been resolved by allowing 1 for as many of the 2023 factors as necessary.
In retrospect, I view this as a fascinating problem in number theory and algebra. Even though I wasn’t able to arrive at the solution independently, I gained valuable insights and enjoyed a robust mental challenge.